협업 필터링을 넘어서: 하이퍼커넥트 AI의 추천 모델링

지난 포스트에서 살펴본 것처럼 추천 시스템은 하이퍼커넥트 비즈니스에서 중요한 역할을 하고 있습니다. 하이퍼커넥트는 50개 이상의 모델을 프로덕션 환경에서 운영 중이며, 그중 다수가 추천 시스템에 활용되고 있습니다. 이번 포스트에서는 하이퍼커넥트 AI 조직이 다양한 추천 엔진에서 어떤 모델링 기법을 적용하고 있는지 소개하고자 합니다¹.

협업 필터링(collaborative filtering)

추천 알고리즘이라고 하면 사람들이 가장 흔히 떠올리는 알고리즘은 협업 필터링(collaborative filtering)입니다(Su et al., 2009; Shi et al., 2014; Koren et al., 2021). 협업 필터링은 2006년 넷플릭스의 추천 시스템을 기존보다 10% 개선한 팀에게 100만 달러의 상금을 제공한 넷플릭스 프라이즈로 유명해졌습니다. 이 알고리즘은 사용자의 과거 선호도를 분석해 비슷한 취향을 가진 다른 사용자들의 데이터를 바탕으로 새로운 아이템에 대한 선호를 예측합니다. 넷플릭스 프라이즈 우승자들이 여러 협업 필터링 알고리즘 중 간단한 행렬 분해(matrix factorization) 방법론만으로도 우승에 근접한 성적을 낼 수 있다는 사실을 밝히면서(Koren et al., 2009) 행렬 분해 기반 협업 필터링 방법론에 대한 관심이 높아졌고 후속 연구들도 활발히 진행되었습니다.

먼저 문제를 조금 더 수학적으로 정의해 보려고 합니다. 협업 필터링은 행렬의 일부 요소(element)만 관측되었을 때, 나머지 관측되지 않은 요소들을 추정하는 문제인 행렬 완성(matrix completion) 문제로 바꿔서 풀 수 있습니다. 유저(행)의 어떤 아이템(열)에 대한 선호도가 행렬의 요소로 표현될 때 관측된 요소들로부터 관측되지 않은 요소들을 추정해 채워 넣을 수 있다면 유저가 경험해 보지 못한 아이템에 대한 선호를 예측할 수 있으며, 이를 통해 추천을 제공할 수 있습니다.

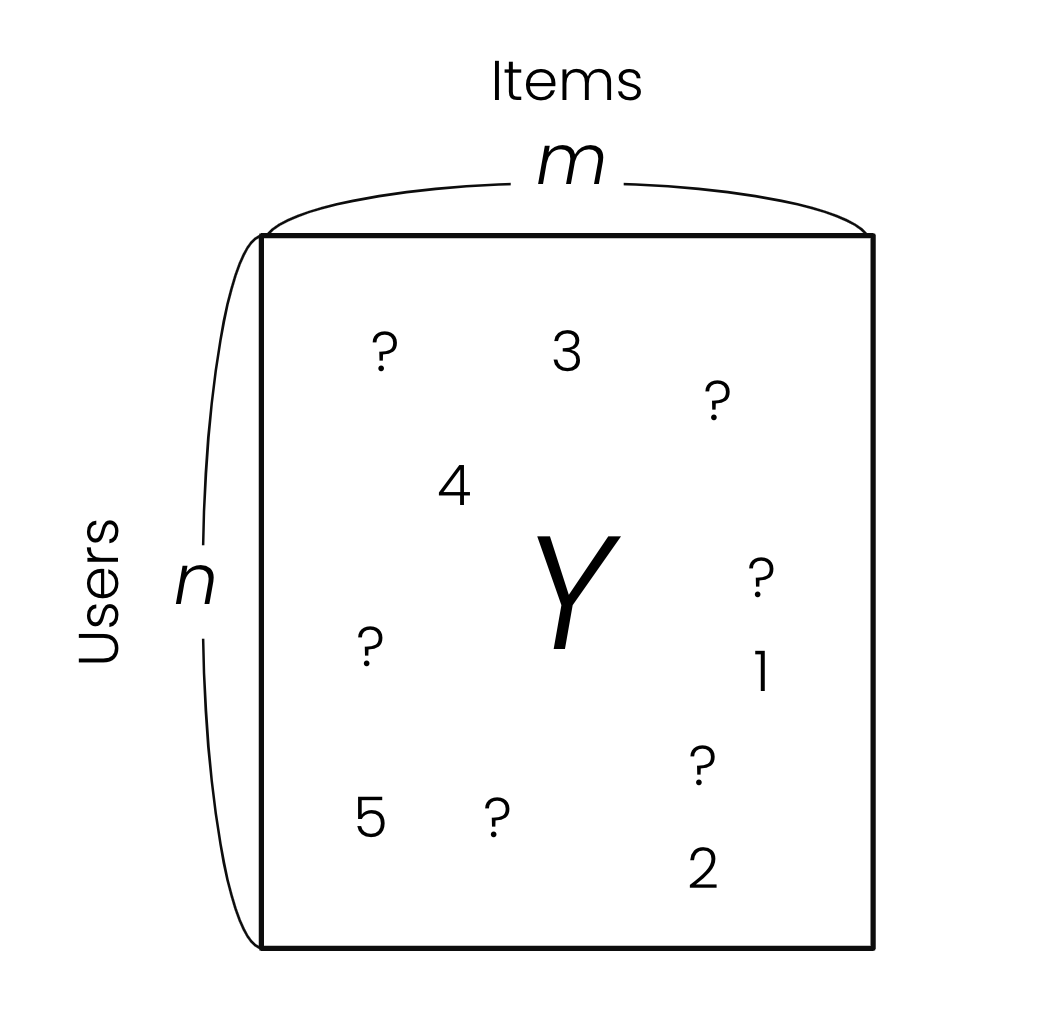
하지만 아무런 가정 없이는 자유도(degree of freedom)가 너무 커서 관측된 요소들만으로는 나머지 요소들을 예측할 수 없습니다. 자유도를 줄이기 위한 여러 가정들이 제안되어 왔지만, 추천 문제에서 흔히 사용되는 가정은 행렬의 랭크 \(k\)가 유저 수 \(n\)과 아이템 수 \(m\)에 비해 매우 작다는 것입니다. 보통 추천 문제에서 \(n\)과 \(m\)은 백만 이상의 값인 데 반해 \(k\)로는 20에서 200 사이의 상대적으로 매우 작은 값이 사용되곤 합니다.

\[\text{rank}(Y)=k \ll \min (n, m)\]

즉, 모든 유저 벡터를 아주 적은 수의 벡터들의 선형 조합(linear combination)으로 표현할 수 있다고 가정하는 것입니다. 한 사람의 취향을 다른 몇몇 사람들의 취향으로 표현할 수 있다고 가정하는 것이므로, 이는 꽤 합리적인 가정으로 받아들여질 수 있습니다. 이를 로우랭크 행렬 완성(low-rank matrix completion) 문제라고 부릅니다.

로우랭크 행렬 완성 문제는 어떻게 풀까?

로우랭크 행렬 완성 문제는 NP-hard 문제로 잘 알려져 있습니다(Meka et al., 2008). 따라서 추가적인 가정 없이는 이 문제를 다항 시간 안에 전역 최적해(global optimum)를 구할 수 없습니다(P ≠ NP일 경우). 그럼에도 불구하고 이 문제의 실용적 가치는 매우 크기 때문에 구해진 해가 전역 최적해가 아니더라도 충분히 유용할 수 있습니다. 이에 따라 뉴클리어 노름(nuclear norm) 최소화(Candes et al., 2012)와 같은 다양한 접근법이 개발되었습니다. 특히 넷플릭스 프라이즈 우승자들의 보고(Koren et al., 2009)를 비롯해 실용적으로 행렬 분해를 활용한 방법들이 추천 문제에서 좋은 성능을 보여주었기에 주목을 받게 되었습니다.

행렬 분해(matrix factorization)

행렬 분해란 무엇일까?

선호도를 나타내는 행렬 \(Y\)의 랭크가 \(k\)일 때 행렬 \(Y\)를 아래와 같이 \(U\)와 \(I\) 행렬로 분해(factorize)할 수 있습니다. 관측된 \(Y\)의 요소들을 통해 \(U\) 와 \(I\)만 정확히 계산하면, \(Y\)의 모든 요소를 예측할 수 있습니다. 이 방법을 행렬 분해라고 하며, 이는 로우랭크 행렬 완성 문제를 해결하는 가장 효과적인 방법 중 하나입니다. 이 행렬 분해 문제의 해를 구하는 방법으로는 크게 교대 최소화(alternating minimization) 방법과 경사 하강(gradient descent) 두 가지가 있습니다.

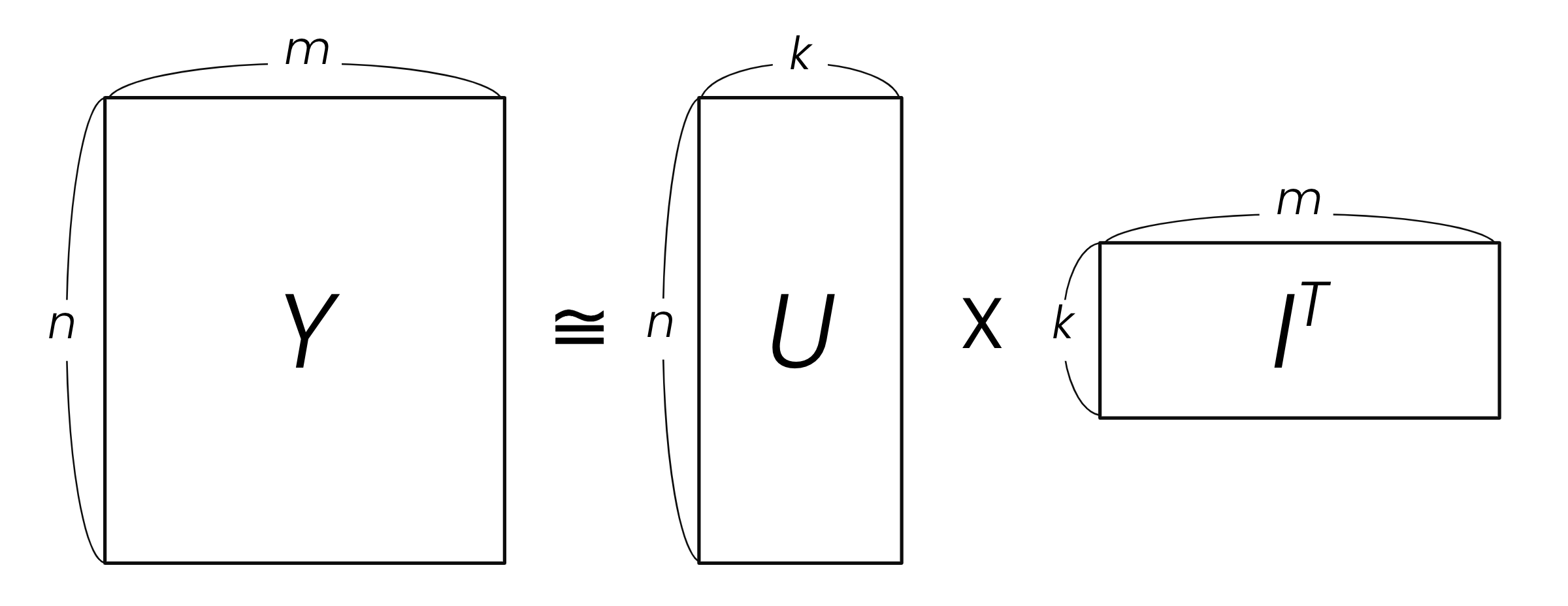
방법 1: 교대 최소화법. 교대 최소화법(Zangwill 1969; Li et al., 2017; Pimentel-Alarcón 2018; Ban et al., 2019)는 가우시안 혼합 모델(Gaussian mixture model)을 포함한 다양한 고전 머신러닝 문제들에서도 널리 쓰이는 방법이며, 여러 파라미터를 동시에 최적화하기 어려울 때 하나의 파라미터를 고정하고 나머지 파라미터를 최적화한 후 그 파라미터를 고정하고 다시 나머지를 최적화하는 과정을 반복하면서 지역 최적해(local optimum)를 찾아갑니다. 행렬 분해 문제에 적용하면 다음과 같은 방법으로 해를 찾게 됩니다.

• 1단계. 먼저, 행렬 \(U\)를 랜덤 초기화합니다.
• 2단계. 행렬 \(U\)가 주어졌을 때 행렬 \(Y\) 중 관측된 요소만을 이용해 행렬 \(I\)를 계산합니다.
• 3단계. 행렬 \(I\)가 주어졌을 때 행렬 \(Y\) 중 관측된 요소만을 이용해 행렬 \(U\)를 계산합니다.
• 4단계. 수렴할 때까지 2단계와 3단계를 반복합니다.

이 방법은 이론적인 수렴 보장은 없지만 실제로는 대부분 수렴하며, 실용적으로 좋은 성과(Besag 1986; Glendinning 1989)를 내어 여러 연구와 산업에서 활용되어 왔습니다. 특히 2단계와 3단계는 선형 회귀(linear regression) 문제로 치환할 수 있어 해석적 해(closed form solution)가 존재하며 선형 회귀를 위한 여러 상용 라이브러리들을 활용할 수 있습니다. 또한, 알고리즘을 약간 수정하면 몇 가지 가정 아래에서 전역 최적해가 지역 최적해와 높은 확률로 가깝다는 것이 증명되기도 했습니다(Jain et al., 2013).

이렇게 교대 최소화법에는 여러 장점이 있지만 한계점도 존재합니다. 행렬 \(Y\)의 크기가 커질수록 연산량이 급격히 증가한다는 문제가 있습니다. 특히, 2단계와 3단계에서 계산해야 하는 해석적 해의 시간 복잡도가 상당히 높습니다. \(n\)이 커지면 연산량이 급격히 증가하며, 역행렬 계산이 포함되어 있어 GPU 연산의 이점을 충분히 활용하기 어렵습니다. 물론, 이러한 단점들을 근사 등의 방법으로 해결하려는 연구들이 있지만, 현실적으로는 다음 방법이 더 간단하며 선호됩니다.

방법 2: 경사 하강법. 행렬 분해의 해를 구하는 또 다른 방법은 경사 하강법입니다. 딥러닝에서 학습을 하는 것처럼 \(U\)와 \(I\) 행렬의 요소를 랜덤으로 초기화하고 그 상태에서 평균 제곱 오차(mean square error; MSE)와 같은 손실 함수를 이용해 경사 하강법 또는 확률적 경사 하강법(stochastic gradient descent; SGD)으로 학습해 나갑니다. 많은 벤치마크 데이터셋들에서 검증해보면 학습이 잘 되고 빠르게 수렴하는 것을 확인할 수 있습니다. 역행렬을 구할 필요가 없으며 PyTorch, Tensorflow 등 라이브러리를 통해 GPU 연산의 이점을 충분히 활용할 수 있는 방법이라 쉽고 빠르게 학습이 가능합니다. 아래는 PyTorch 라이브러리를 사용해 행렬 분해를 SGD로 학습하는 간단한 코드 스니펫입니다.

class MatrixFactorization(nn.Module):
    def __init__(self, n, m, k):
        super(MatrixFactorization, self).__init__()
        self.U = nn.Embedding(n, k)
        self.I = nn.Embedding(m, k)

    def forward(self, u, i):
        U = self.U(u)
        I = self.I(i)
        return (U * I).sum(1)

model = MatrixFactorization(n, m, k)
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=learning_rate)

for epoch in range(num_epochs):
    total_loss = 0
    for u, i, y in data:
        optimizer.zero_grad()
        prediction = model(u, i)
        loss = criterion(prediction, y.float())
        loss.backward()
        optimizer.step()
        total_loss += loss.item()

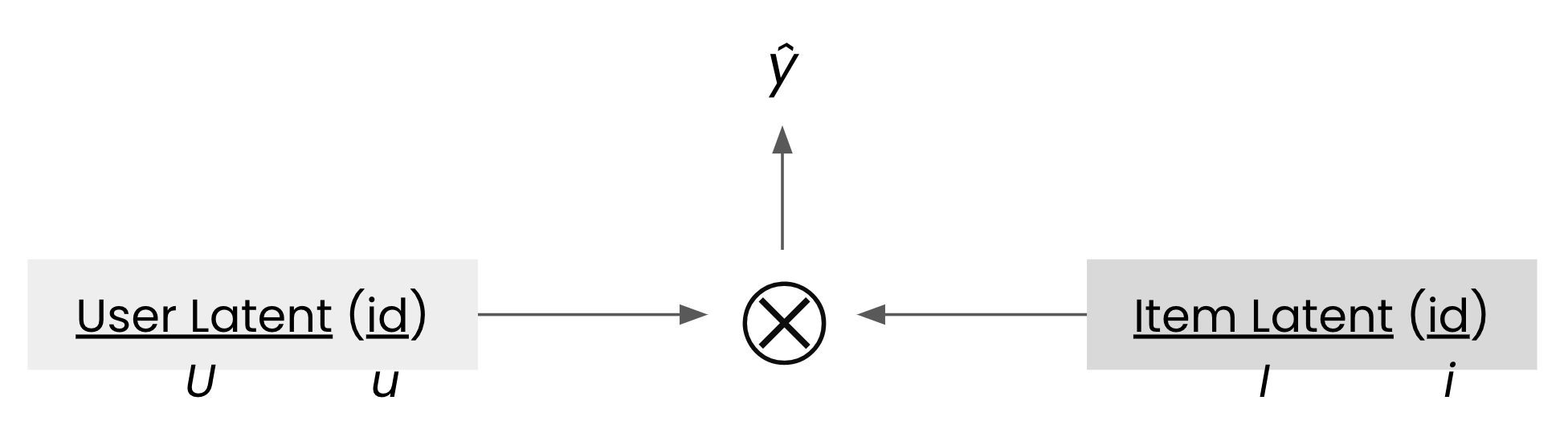
위 코드에서 모델을 그림으로 표현하면 아래와 같이 도식화할 수 있습니다. 유저 아이디 \(u\)와 아이템 아이디 \(i\)가 입력으로 주어지면 행렬 \(U\)와 \(I\)에서 각각 \(u\)와 \(i\)에 해당하는 벡터들을 추출하고 이를 내적하여 최종 예측값 \(\hat{y}\)를 계산합니다.

경사 하강법 역시 교대 최소화법과 마찬가지로 이론적으로 검증된 방식입니다. 경사 하강법의 학습은 교대 최소화법과 최소로 필요한 요소의 수가 점근적으로(asymptotically) 비슷합니다(Keshavan et al., 2010). 추가 연구들(Keshavan et al., 2010; Ge et al., 2016; Bhojanapalli et al., 2016; Ge et al., 2017)에 따르면 랜덤 초기화에 좋은 성질이 있다는 것이 밝혀졌고 몇 가지 가정을 추가하면 랜덤 초기화만으로도 지역 최적해가 전역 최적해와 충분히 가까울 수 있다는 것이 증명되었습니다². 또한, 경사 하강법은 실용적으로도 효과가 입증되었습니다. 여러 연구들(Lee et al., 2013; Yuan et al., 2014; Chen et al., 2015; Chen et al., 2016a; Li et al., 2016)에 따르면 SGD를 통해 협업 필터링 문제들을 푸는 벤치마크 데이터셋에서 각 연구가 당시 기준의 SotA(state-of-the-art)를 달성했습니다. 이러한 근거를 바탕으로 하이퍼커넥트 AI 조직에서는 주로 SGD 방식을 사용하고 있습니다. 대용량 데이터를 간편하게 처리할 수 있으며 성능적으로도 우수한 결과를 나타내기 때문입니다.

하지만, 이때 주의할 점은 가중치 감쇠(weight decay)를 통한 정규화가 반드시 필요하다는 것입니다. 이론적으로도 가중치 감쇠의 필요성을 언급한 연구들(Mnih et al., 2007; Bhojanapalli et al., 2016; Ge et al., 2017)이 있었을 뿐만 아니라, 실제 데이터에 모델을 적용하면 가중치 감쇠 하이퍼파라미터를 어떻게 사용하느냐에 따라 성능이 크게 달라지는 모습을 관찰할 수 있기 때문에 가중치 감쇠를 적절히 활용하는 것이 필수적입니다. 그뿐만 아니라 현실에서는 행렬 \(Y\)에 대한 관측이 균일하지 않습니다. 어떤 유저들은 서비스를 집중적으로 사용해 선호도 데이터를 많이 남기지만, 다른 유저들은 적게 남깁니다. 모든 파라미터에 동일한 가중치 감쇠 하이퍼파라미터를 적용하면, 한쪽이 오버피팅되거나 다른 쪽이 언더피팅되는 경우가 발생할 수 있기 때문에 SGD를 통한 학습에서는 이러한 문제가 더 자주 발생할 수 있음을 인지하고 SGD를 사용할 때는 다양한 방법들(Li et al., 2017; Chen et al., 2019; Yi et al., 2021)을 추가로 고려해야 합니다.

행렬 분해의 추상화

머신러닝 모델을 다룰 때 입력과 출력을 먼저 정의하고 내부를 추상화하여 생각하면 새로운 발견을 할 수 있는 경우가 많습니다. 행렬 분해도 입력과 출력을 기준으로 추상화하면 아래와 같은 형태로 표현할 수 있습니다.

\[\hat{y} = f(u, i)\]

유저 아이디 \(u\)와 아이템 아이디 \(i\)가 주어졌을 때 선호도 \(\hat{y}\)를 예측하는 함수를 구하는 모델을 행렬 분해라고 정의할 수 있습니다. 함수 \(f\)는 행렬 \(U\)와 \(I\)로 파라미터화된 것으로 볼 수 있습니다. 행렬 분해 알고리즘에는 또한 수많은 변형들(Lee et al., 2013; Yuan et al., 2014; Chen et al., 2015; Chen et al., 2016a; Li et al., 2016)이 존재합니다. 각 변형들마다 함수 \(f\)가 어떻게 파라미터화되는지 차이가 있지만 모두 위와 같은 형태로 추상화된 표현이 가능합니다.

뉴럴 네트워크로의 확장

한편, 최근 10여 년간 머신러닝 분야에서 딥러닝이 활발하게 사용되고 있습니다. 협업 필터링에서도 뉴럴 네트워크를 적용한 연구들이 많이 발표되었으며 최근에도 활발히 진행되고 있습니다. 몇몇 대표적인 연구를 살펴보며 하이퍼커넥트 AI 조직이 사용하는 추천 모델링 방법을 구체적으로 소개하겠습니다.

NCF(He et al., 2017). NCF(neural collaborative filtering)는 행렬 분해를 뉴럴 네트워크로 확장한 가장 단순한 형태입니다. 행렬 분해를 경사 하강법으로 학습하는 것이 안정적으로 잘 동작한다는 것이 경험적으로나 이론적으로 입증되었기 때문에 확장할 수 있는 방법입니다².

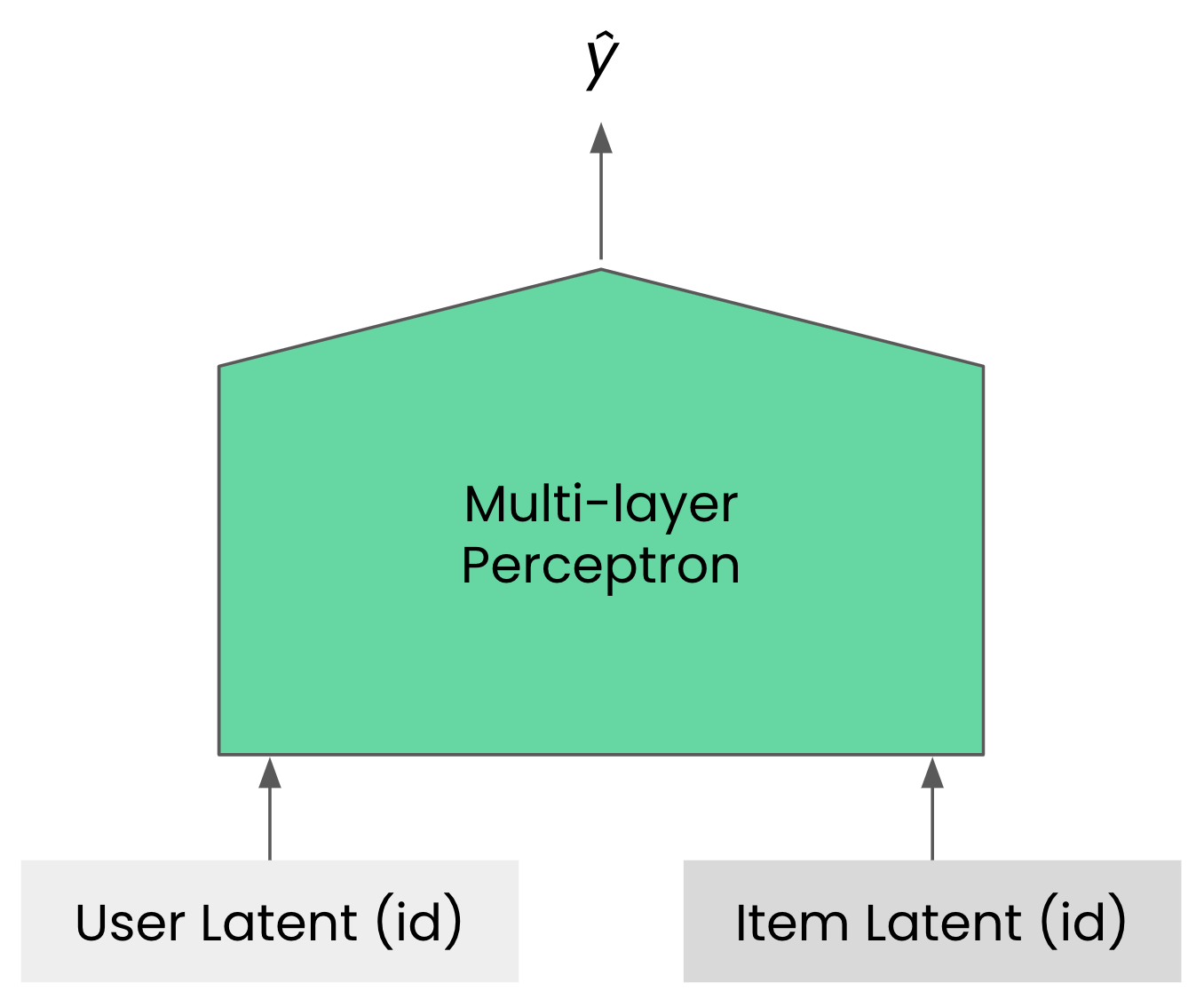
유저 벡터와 아이템 벡터의 단순 내적이 행렬 분해라면, NCF는 내적 대신 다층 퍼셉트론(multi-Layer perceptron)을 사용해 표현력을 향상시킵니다(Hornik et al., 1989)³. 이 모델을 구현하려면 유저 임베딩 벡터의 차원을 설정해야 합니다. 이 차원은 행렬 분해의 랭크와 대응한다고 볼 수 있습니다.

\[\hat{y} = f(u, i)\]

행렬 분해와 마찬가지로 NCF도 위와 같이 추상화해서 표현할 수 있습니다. 따라서 본 모델로의 확장까지는 추상화 결과에 큰 변화가 있지는 않지만, 다음에 소개할 모델의 확장 방향은 행렬 분해와는 다른 새로운 관점을 제공합니다.

AutoRec(Sedhain et al., 2015). 이 논문은 오토인코더(autoencoders)의 아이디어를 응용해 협업 필터링 문제를 해결하는 것이지만, 유저가 특정 아이템에 대해 가지는 선호를 예측하기 위해 아래 그림과 같은 모델을 사용하는 방식으로도 이해할 수 있습니다.

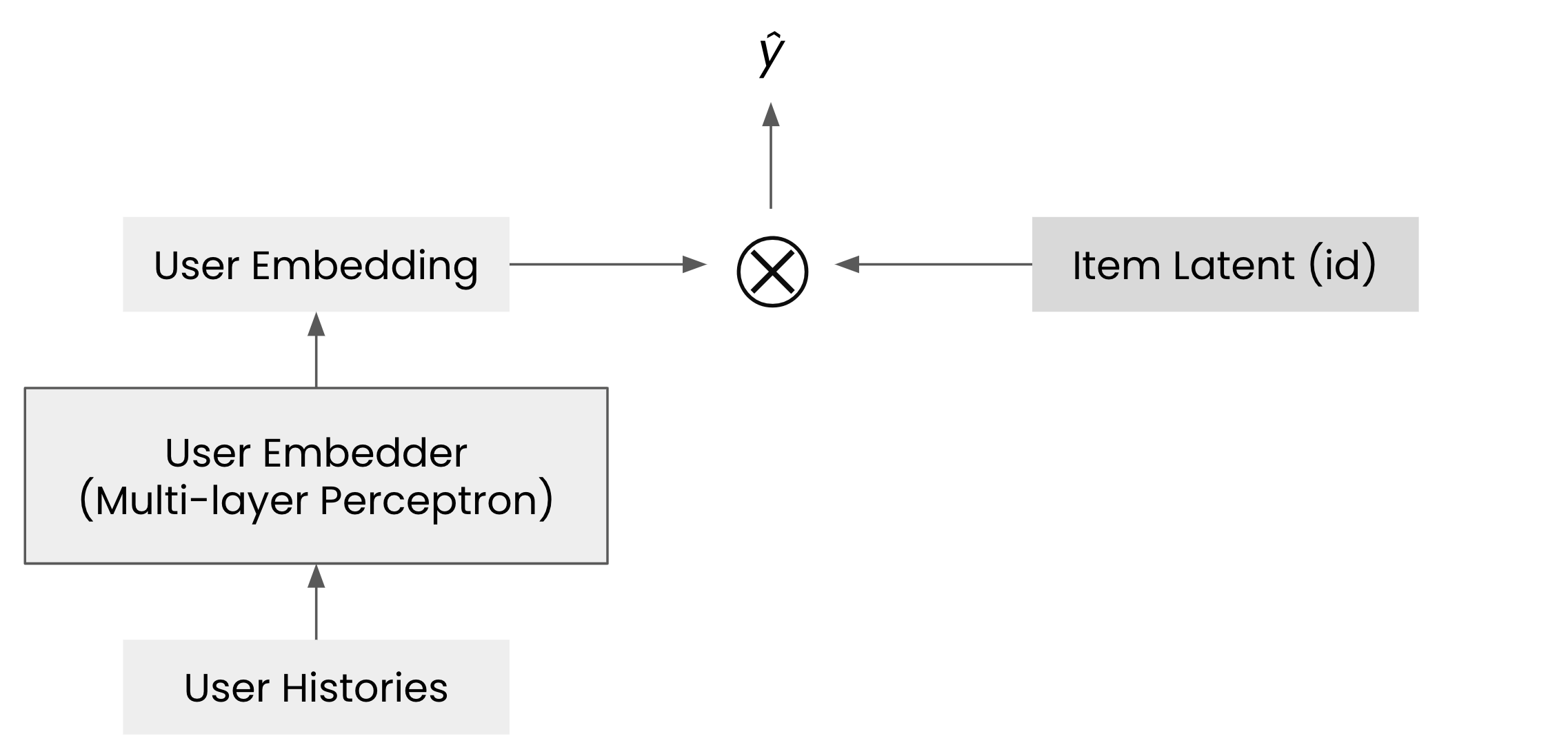
행렬 분해와 NCF가 유저 벡터와 아이템 벡터에 단순 내적(또는 내적의 일반화된 연산)을 취하는 방식이었다면, AutoRec 모델은 유저 벡터를 미리 선언된 행렬(임베딩)에서 단순히 조회(look-up)하는 방식이 아닌 해당 유저가 경험했던 아이템들의 히스토리 \(\mathcal{H}_u\) 를 입력하는 방식입니다. 즉 AutoRec 모델은 유저의 히스토리 \(\mathcal{H}_u\)와 아이템 아이디 \(i\)를 입력으로 받아 선호도 \(\hat{y}\)를 예측하는 방식이라고 볼 수 있습니다. 이를 추상화하면 다음과 같습니다.

\[\hat{y} = f(\mathcal{H}_u, i)\]

자연스럽게 아이템의 히스토리 \(\mathcal{H}_i\) 와 유저 아이디 \(u\)를 입력으로 받아 선호도 \(\hat{y}\)를 예측하는 대칭적인 모델도 함께 제안되었습니다.

\[\hat{y} = f(u, \mathcal{H}_i)\]

이후 AutoRec 논문의 다양한 변형들이 제안되었으며(Zheng et al., 2016; Liang et al., 2018; Sachdeva et al., 2019; Vančura et al., 2022; Liu et al., 2023; Spišák et al., 2023) 그중 일부는 당시 SotA를 달성할 정도로 성능이 우수했습니다. 한편, CF-UIcA(Du et al., 2018)는 AutoRec 모델을 확장해 다음과 같은 모델을 제안했습니다.

\[\hat{y} = f(\mathcal{H}_u, \mathcal{H}_i)\]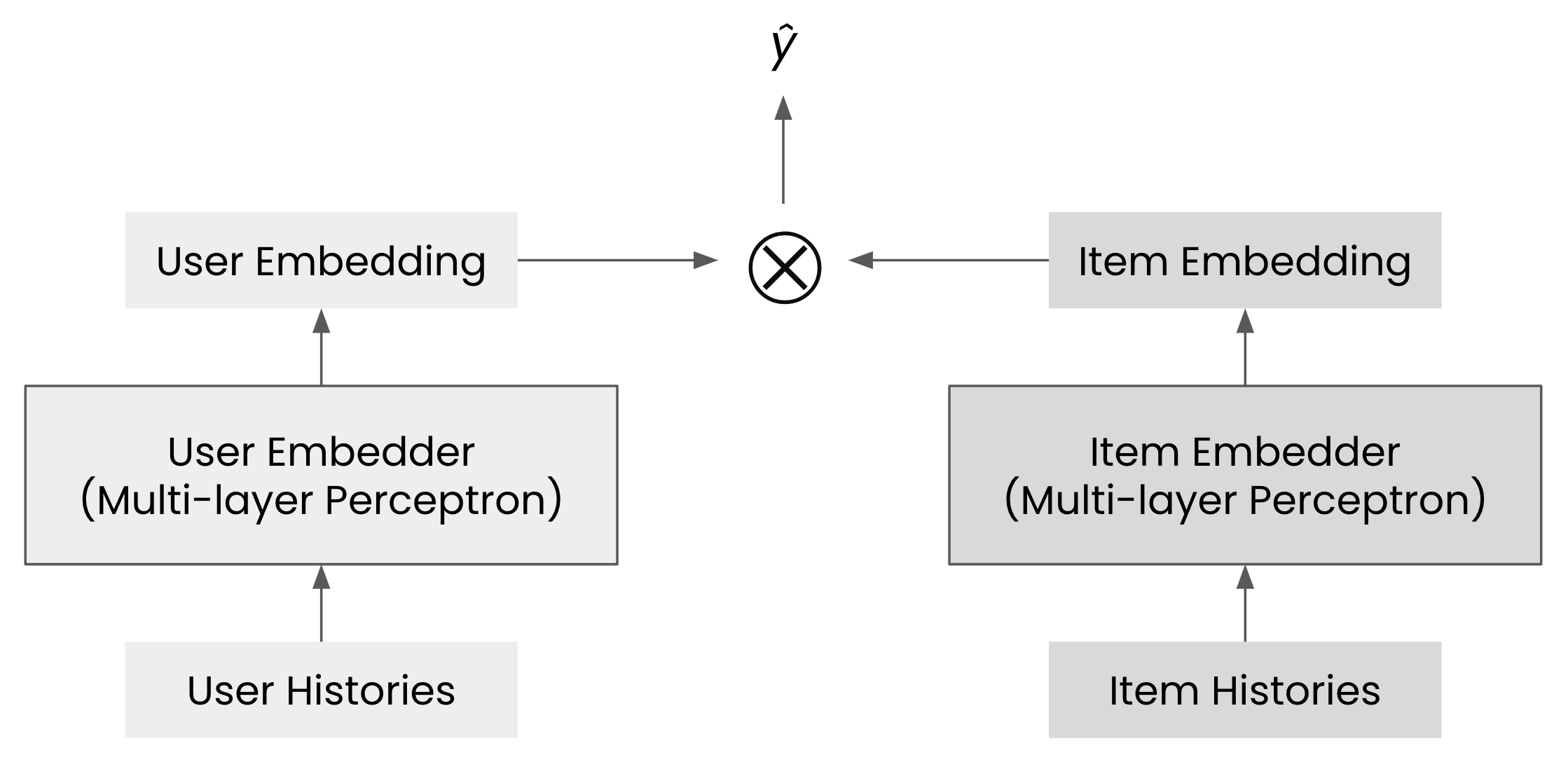

함수의 입력으로 유저나 아이템 한쪽만 히스토리를 받는 것이 아니라, 유저와 아이템 양쪽 모두의 히스토리를 입력으로 받아 성능 향상을 기대했습니다. 실제로 CF-UIcA 모델은 당시 SotA를 달성했고요.

하이퍼커넥트 AI 조직의 추천 모델링(1/2)

하이퍼커넥트 AI 조직에서는 기존 연구를 폭넓게 조사하고 각 연구를 추상화된 형태로 사고하는 것을 강력히 장려하고 있습니다. 각 연구가 어떤 형태로 추상화될 수 있는지 고민하다 보면, 최적에 가까운 모델링을 할 수 있기 때문입니다. 본 경우에도 마찬가지입니다. 위에서 기술한 것처럼 기존 연구를 추상화하면 대부분의 모델이 아래 네 가지 중 하나에 해당하게 됩니다.

\[\hat{y} = f(u, i), \hat{y} = f(\mathcal{H}_u, i), \hat{y} = f(u, \mathcal{H}_i), \hat{y} = f(\mathcal{H}_u, \mathcal{H}_i)\]

그럼 이런 생각을 해볼 수 있습니다.

우리는 위 모델들의 입력을 통합해서 모델링해 볼 수는 없을까?

입력이 다양해질수록 모델이 활용할 수 있는 정보도 많아집니다. 함수 \(f\)가 제대로 학습되면 입력이 추가될수록 성능이 향상되어야 합니다. 적어도 성능이 떨어지지는 않아야 합니다. 유저를 함수 \(f\)의 입력으로 넣을 때 \(u\)만 넣거나 \(\mathcal{H}_u\)만 넣는 것이 아니라 \(u\)와 \(\mathcal{H}_u\)를 같이 \(f\)의 입력으로 넣으면 성능이 더 좋아질 것으로 기대할 수 있습니다. 아이템을 입력으로 넣을 때에도 마찬가지고요. 실제로 하이퍼커넥트는 이런 아이디어를 바탕으로 \(u\), \(\mathcal{H}_u\), \(i\), \(\mathcal{H}_i\)를 모두 함수의 입력으로 넣고 있습니다.

\[\hat{y} = f(u, \mathcal{H}_u,i, \mathcal{H}_i)\]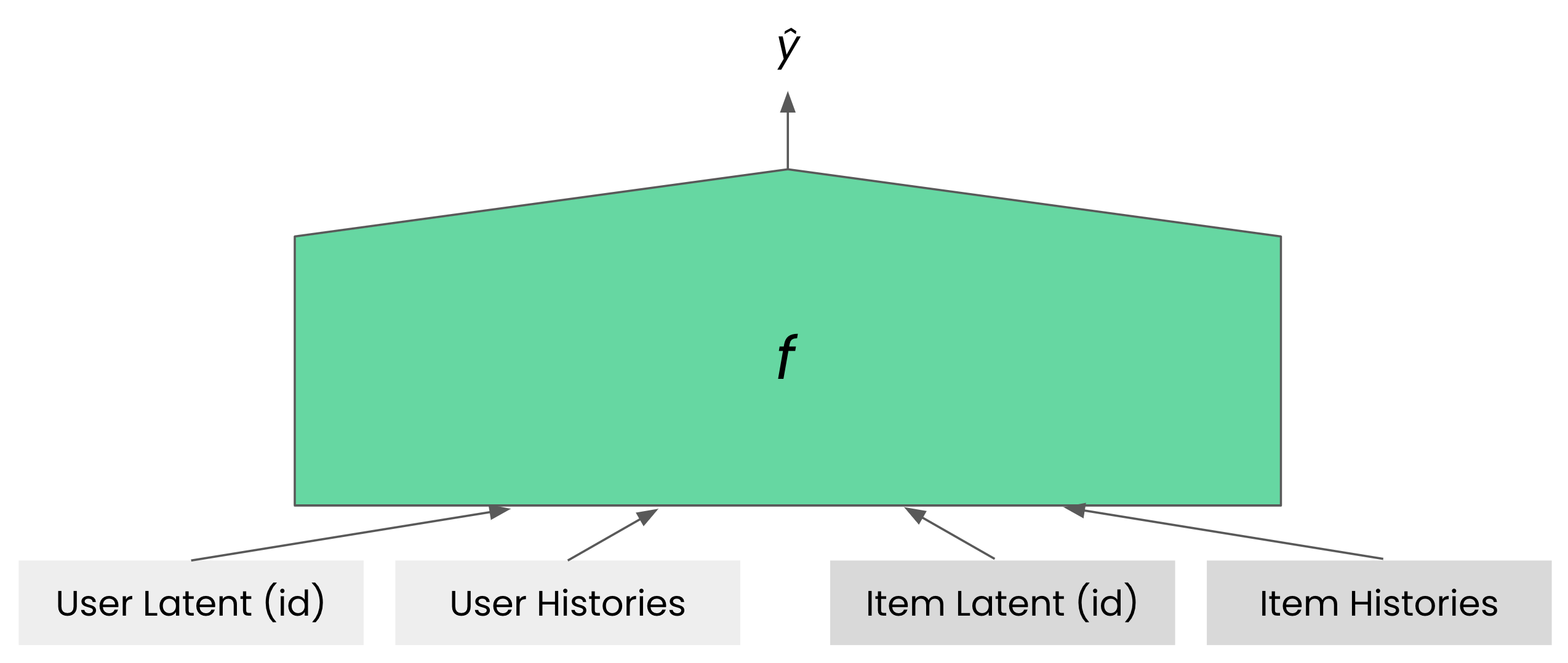

협업 필터링에 대한 문헌들을 조사하다 보면 AutoRec이나 CF-UIcA 형태에서도 더 일반화된 모델들이 존재한다는 것을 쉽게 알 수 있습니다. 그중 하나가 그래프 뉴럴 네트워크(graph neural networks; GNN) 방향으로의 확장인데요. 대표적으로 GCMC(Berg et al., 2017)가 있고 GCMC는 AutoRec, CF-UIcA의 일반화된 형태임을 보일 수 있습니다. 하지만, 아쉽게도 GCMC는 위에서 계속 설명해 온 것처럼 \(\hat{y} = f( \cdot )\) 형태로 표현할 수 없습니다. GCMC 등 GNN 계열 모델들의 아이디어를 반영하기 위해서는 새로운 방식의 추상화가 필요합니다. 하지만, 하이퍼커넥트 AI는 2024년 현재 GNN 계열들에서 제안하는 아이디어들을 추천 모델링에 반영하고 있지 않습니다. GNN 계열들이 학계에서 많은 연구가 되고 있는 것은 사실이나 벤치마크 데이터셋에서 우수한 성능을 보인다는 것이 아직 충분히 입증되지 않았으며, 배포 시나리오도 복잡하기에 다른 기술들을 검토하는 것이 더 우선순위가 높다고 판단했기 때문입니다.

보조 정보(side information)

서비스를 운영하다 보면 유저의 국가, 성별, 플랫폼(안드로이드/iOS) 등 다양한 추가 정보가 자연스럽게 쌓입니다⁴. 추천 알고리즘을 만들 때 이러한 추가 데이터를 활용해 성능을 향상시키는 것은 당연한 일입니다. 학계에서는 이미 이 문제를 보조 정보(side information 혹은 auxiliary information)를 추천 알고리즘에 통합하는 문제로 정의해왔습니다(Menon et al., 2011; Lee et al., 2017; Volkovs et al., 2017; Shin et al., 2023). 특히 이러한 보조 정보는 유저의 기존 히스토리 데이터가 부족한 신규 유저에게 특히 추천 성능을 향상시키는 데 큰 도움이 됩니다(Schein et al., 2002; Saraswathi et al., 2017; Rama et al., 2019; Abdullah et al., 2021; Sethi et al., 2021; Panda et al., 2022; Berisha et al., 2023).

보조 정보를 이용해 추천 성능을 높이는 수많은 모델이 존재하지만 가장 유명한 것 중 하나는 FM(factorization machines; Rendle 2010)입니다. 변형인 FFM(field-aware factorization machines; Juan et al., 2016)이 여러 챌린지에서 우승하면서 본격적으로 주목을 받기 시작했는데요. FM은 SVM(support vector machines)에서 모티브를 얻었으나, 행렬 분해의 또 다른 일반화로 볼 수 있습니다. 유저 아이디와 보조 정보를 같이 활용하는 FM을 \(\hat{y} = f( \cdot )\) 꼴로 추상화해서 표현하면 다음과 같습니다.

\[\hat{y} = f(u, \mathcal{S}_u,i, \mathcal{S}_i)\]

\(\mathcal{S}_u\)는 유저 \(u\)의 보조 정보입니다. FM의 후속으로 클릭률 예측 등의 다양한 도메인에서 여러 모델(Juan et al., 2016; Guo et al., 2017; Lian et al., 2018; Song et al., 2019)들이 등장했고 이들 역시 위와 같은 추상화된 형태로 표현할 수 있었습니다.

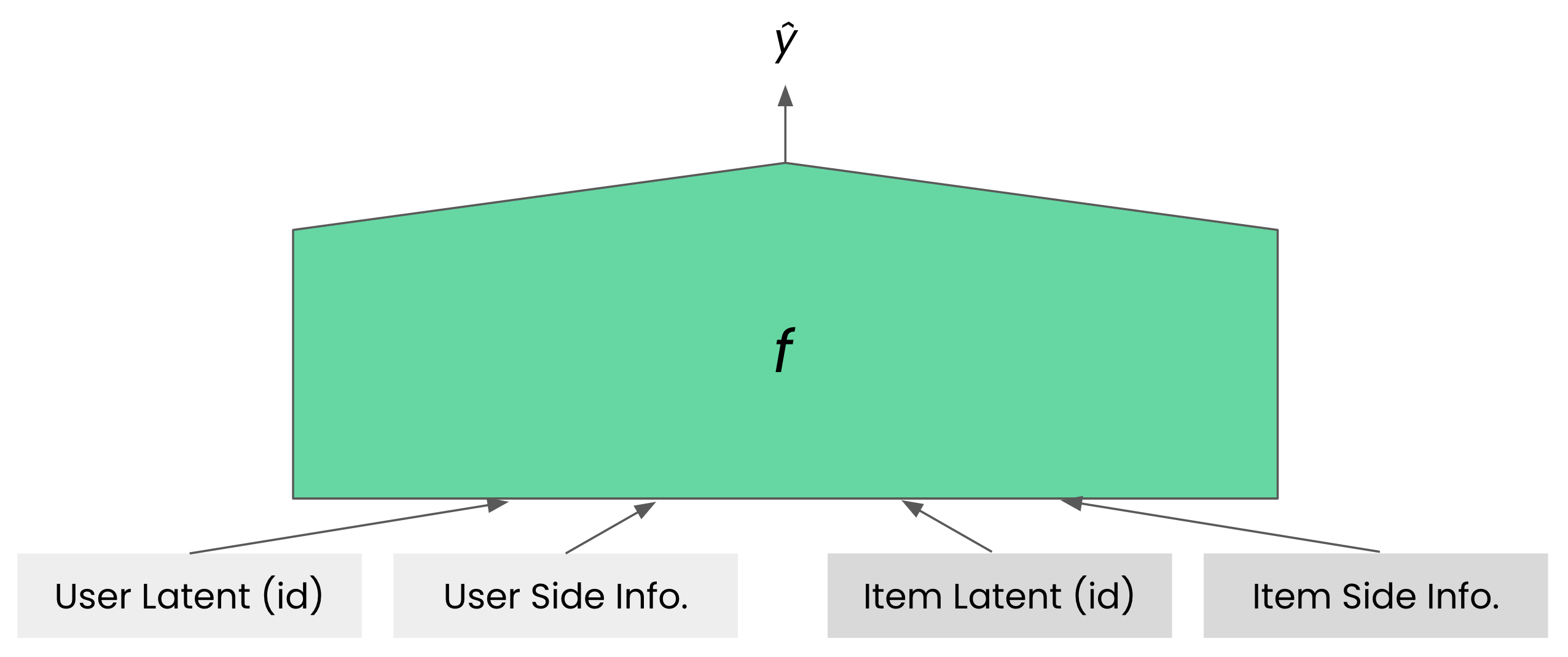
특별히 언급하고 싶은 것은 \(\hat{y} = f(u, \mathcal{S}_u,i, \mathcal{S}_i)\)에서의 함수 \(f\)가 추천 모델들로만 모델링되어야 하는 것은 아니라는 점입니다. 입력을 테이블 데이터로 보고 이 문제를 테뷸러 러닝(tabular learning)으로 정의해 풀 수도 있는데요. 뉴럴 네트워크로 테이블 형태의 데이터를 학습하는 여러 가지 방법들(Popov et al., 2019; Huang et al., 2020; Arik et al., 2021; Borisov et al., 2022; Wang et al., 2022)이 있지만, 아직은 그라디언트 부스팅(Chen et al., 2016; Ke et al., 2017; Prokhorenkova et al., 2018)이 좋은 성과를 나타내고 있습니다. 특히, 2020년 열린 RecSys 챌린지에서는 XGBoost(Chen et al., 2016)를 활용한 팀(Schifferer et al., 2020)이 우승을 차지했고요. 여러 추천 벤치마크 데이터셋들에서 그라디언트 부스팅 알고리즘들이 뉴럴 네트워크 기반 방법론들을 월등히 뛰어넘는 성능을 보여주기도 했습니다(Yi et al., 2021a). 실제로 하이퍼커넥트는 과거에 CatBoost(Prokhorenkova et al., 2018)를 추천 모델 중의 한 종류로 사용하고 있음을 공개하기도 했었고요.

하이퍼커넥트 AI 조직의 추천 모델링(2/2)

앞서 하이퍼커넥트 AI 조직의 추천 모델링(1/2)에서 제안한 모델링에 보조 정보를 추가해 최종적으로 하이퍼커넥트 AI는 다음과 같은 모델을 대부분의 추천 시스템에서 사용하고 있습니다.

\[\hat{y} = f(u, \mathcal{H}_u, \mathcal{S}_u,i,\mathcal{H}_i, \mathcal{S}_i)\]

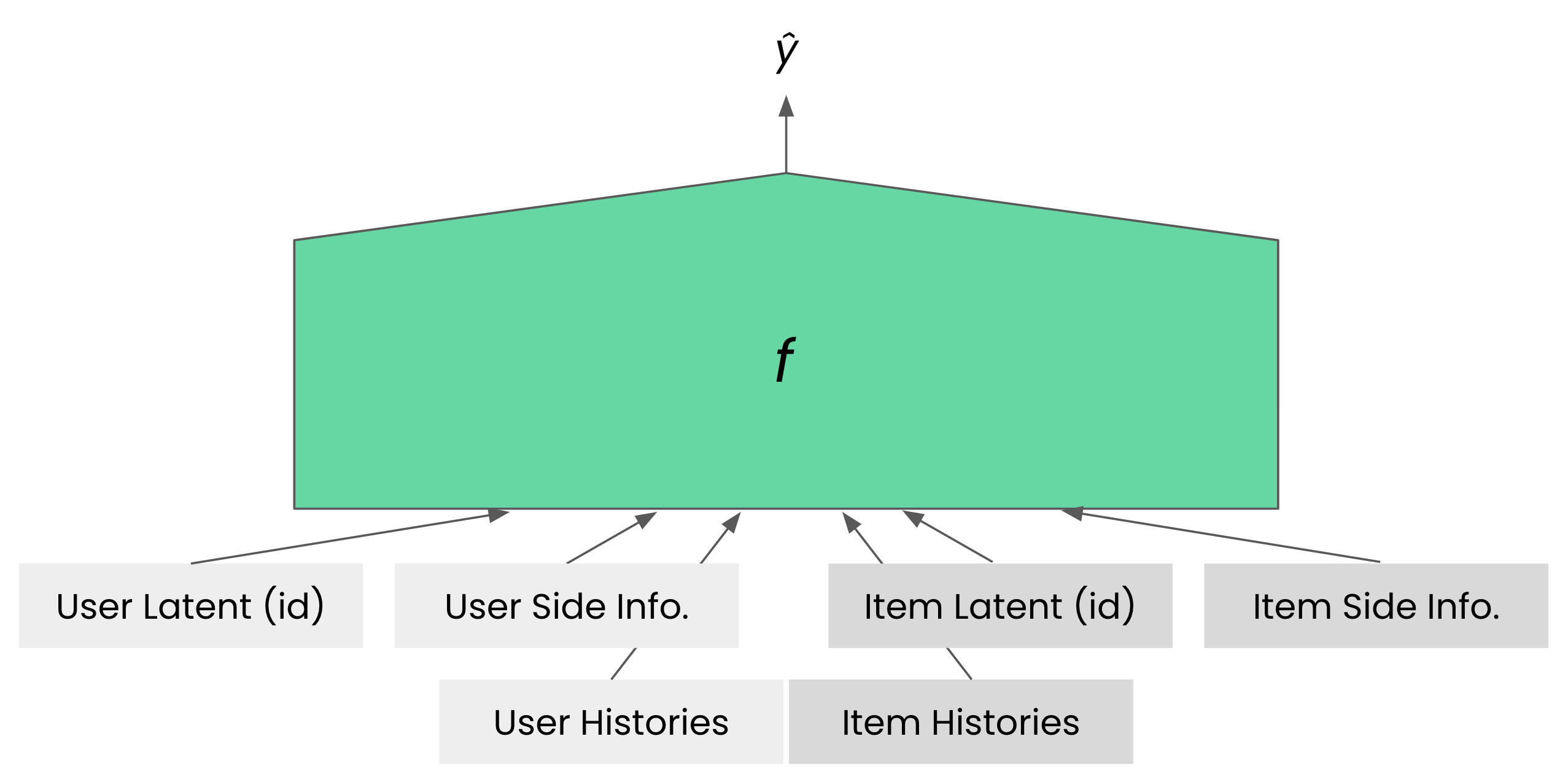
정말 다양한 곳에 추천 모델을 운용하고 있기에 \(f\)에 어떤 모델을 사용하는지는 목적에 따라 다양합니다. 선형 모델, 과거에 공개된 CatBoost 모델, 작은 뉴럴 네트워크 모델 등을 사용하며 어떤 문제에서는 GPT 스케일의 대형 트랜스포머 모델도 사용하고 있습니다.

이번 포스트에서는 하이퍼커넥트 AI 조직이 추천 모델링에서 기본적으로 어떤 접근을 취하고 있는지 알아보았습니다. 하이퍼커넥트 AI 조직은 여러 문헌 조사 결과를 바탕으로 이론적으로도 실용적으로도 효과가 입증된 경사 하강 학습 방법론을 추천 모델링에 주로 사용하기로 결정했습니다. 또한 여러 협업 필터링 연구에서 얻은 통찰을 바탕으로 행렬 분해나 NCF, AutoRec 같은 모델을 직접적으로 활용하는 대신 사용자와 아이템의 아이디, 히스토리, 그리고 보조 정보를 모두 활용하는 모델링 방식을 채택하고 있습니다. 하이퍼커넥트는 여러 문헌 조사를 바탕으로 문제와 모델을 추상화해서 생각하고 그것들을 바탕으로 어떤 모델이 최적의 선택인지 고민하며 그 결과를 프로덕션에 녹여내고 있습니다. 다음 포스트에서는 조금 더 구체적으로 아자르 1:1 매치메이킹에 어떤 추천 모델이 사용되고 있는지 알아보고자 합니다.

---

¹ 하이퍼커넥트의 많은 추천 문제들은 유저에게 다른 유저를 추천해 주는 상호 추천(reciprocal recommendation)을 다루지만, 본 포스트에서는 설명의 편의를 위해 유저에게 아이템을 추천해 주는 일반적인 추천 설정을 기준으로 설명하겠습니다.

² 본 모델은 해석적 해가 존재하지 않으므로 교대 최소화 방법을 사용할 수 없습니다.

³ 물론 다층 퍼셉트론이 제대로 내적 연산을 일반화하지 못한다는 연구도 존재합니다(Rendle et al., 2020).

⁴ 너무나 당연하게도 하이퍼커넥트는 유저의 개인 정보를 최우선으로 중요하게 생각합니다. 민감한 유저 정보는 절대 수집하지 않으며 추천 알고리즘에 활용하지 않습니다.

Reference

• (Zangwill 1969) Zangwill, W. I. (1969). Nonlinear programming: a unified approach.

• (Besag 1986) Besag, J. (1986). On the statistical analysis of dirty pictures. Journal of the Royal Statistical Society Series B: Statistical Methodology, 48(3), 259-279.

• (Glendinning 1989) Glendinning, R. H. (1989). An evaluation of the ICM algorithm for image reconstruction. Journal of Statistical Computation and Simulation, 31(3), 169-185.

• (Hornik et al., 1989) Hornik, K., Stinchcombe, M., & White, H. (1989). Multilayer feedforward networks are universal approximators. Neural networks, 2(5), 359-366.

• (Tibshirani et al., 1996) Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society Series B: Statistical Methodology, 58(1), 267-288.

• (Schein et al., 2002) Schein, A. I., Popescul, A., Ungar, L. H., & Pennock, D. M. (2002, August). Methods and metrics for cold-start recommendations. In Proceedings of the 25th annual international ACM SIGIR conference on Research and development in information retrieval (pp. 253-260).

• (Mnih et al., 2007) Mnih, A., & Salakhutdinov, R. R. (2007). Probabilistic matrix factorization. Advances in neural information processing systems, 20.

• (Meka et al., 2008) Meka, R., Jain, P., Caramanis, C., & Dhillon, I. S. (2008, July). Rank minimization via online learning. In Proceedings of the 25th International Conference on Machine learning (pp. 656-663).

• (Koren et al., 2009) Koren, Y., Bell, R., & Volinsky, C. (2009). Matrix factorization techniques for recommender systems. Computer, 42(8), 30-37.

• (Su et al., 2009) Su, X., & Khoshgoftaar, T. M. (2009). A survey of collaborative filtering techniques. Advances in artificial intelligence, 2009.

• (Keshavan et al., 2010) Keshavan, R. H., Montanari, A., & Oh, S. (2010). Matrix completion from a few entries. IEEE transactions on information theory, 56(6), 2980-2998.

• (Rendle 2010) Rendle, S. (2010, December). Factorization machines. In 2010 IEEE International conference on data mining (pp. 995-1000). IEEE.

• (Menon et al., 2011) Menon, A. K., Chitrapura, K. P., Garg, S., Agarwal, D., & Kota, N. (2011, August). Response prediction using collaborative filtering with hierarchies and side-information. In Proceedings of the 17th ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 141-149).

• (Candes et al., 2012) Candes, E., & Recht, B. (2012). Exact matrix completion via convex optimization. Communications of the ACM, 55(6), 111-119.

• (Jain et al., 2013) Jain, P., Netrapalli, P., & Sanghavi, S. (2013, June). Low-rank matrix completion using alternating minimization. In Proceedings of the forty-fifth annual ACM symposium on Theory of computing (pp. 665-674).

• (Lee et al., 2013) Lee, J., Kim, S., Lebanon, G., & Singer, Y. (2013, May). Local low-rank matrix approximation. In International conference on machine learning (pp. 82-90). PMLR.

• (Shi et al., 2014) Shi, Y., Larson, M., & Hanjalic, A. (2014). Collaborative filtering beyond the user-item matrix: A survey of the state of the art and future challenges. ACM Computing Surveys (CSUR), 47(1), 1-45.

• (Yuan et al., 2014) Yuan, T., Cheng, J., Zhang, X., Qiu, S., & Lu, H. (2014, June). Recommendation by mining multiple user behaviors with group sparsity. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 28, No. 1).

• (Chen et al., 2015) Chen, C., Li, D., Zhao, Y., Lv, Q., & Shang, L. (2015, August). WEMAREC: Accurate and scalable recommendation through weighted and ensemble matrix approximation. In Proceedings of the 38th international ACM SIGIR conference on research and development in information retrieval (pp. 303-312).

• (Sedhain et al., 2015) Sedhain, S., Menon, A. K., Sanner, S., & Xie, L. (2015, May). Autorec: Autoencoders meet collaborative filtering. In Proceedings of the 24th international conference on World Wide Web (pp. 111-112).

• (Bhojanapalli et al., 2016) Bhojanapalli, S., Neyshabur, B., & Srebro, N. (2016). Global optimality of local search for low rank matrix recovery. Advances in Neural Information Processing Systems, 29.

• (Chen et al., 2016) Chen, T., & Guestrin, C. (2016, August). Xgboost: A scalable tree boosting system. In Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining (pp. 785-794).

• (Chen et al., 2016a) Chen, C., Li, D., Lv, Q., Yan, J., Chu, S. M., & Shang, L. (2016, July). MPMA: Mixture Probabilistic Matrix Approximation for Collaborative Filtering. In IJCAI (pp. 1382-1388).

• (Ge et al., 2016) Ge, R., Lee, J. D., & Ma, T. (2016). Matrix completion has no spurious local minimum. Advances in neural information processing systems, 29.

• (Juan et al., 2016) Juan, Y., Zhuang, Y., Chin, W. S., & Lin, C. J. (2016, September). Field-aware factorization machines for CTR prediction. In Proceedings of the 10th ACM conference on recommender systems (pp. 43-50).

• (Li et al., 2016) Li, D., Chen, C., Lv, Q., Yan, J., Shang, L., & Chu, S. (2016, June). Low-rank matrix approximation with stability. In International Conference on Machine Learning (pp. 295-303). PMLR.

• (Zheng et al., 2016) Zheng, Y., Tang, B., Ding, W., & Zhou, H. (2016, June). A neural autoregressive approach to collaborative filtering. In International Conference on Machine Learning (pp. 764-773). PMLR.

• (Berg et al., 2017) Berg, R. V. D., Kipf, T. N., & Welling, M. (2017). Graph convolutional matrix completion. arXiv preprint arXiv:1706.02263.

• (Ge et al., 2017) Ge, R., Jin, C., & Zheng, Y. (2017, July). No spurious local minima in nonconvex low rank problems: A unified geometric analysis. In International Conference on Machine Learning (pp. 1233-1242). PMLR.

• (Guo et al., 2017) Guo, H., Tang, R., Ye, Y., Li, Z., & He, X. (2017). DeepFM: a factorization-machine based neural network for CTR prediction. arXiv preprint arXiv:1703.04247.

• (He et al., 2017) He, X., Liao, L., Zhang, H., Nie, L., Hu, X., & Chua, T. S. (2017, April). Neural collaborative filtering. In Proceedings of the 26th international conference on world wide web (pp. 173-182).

• (Ke et al., 2017) Ke, G., Meng, Q., Finley, T., Wang, T., Chen, W., Ma, W., … & Liu, T. Y. (2017). Lightgbm: A highly efficient gradient boosting decision tree. Advances in neural information processing systems, 30.

• (Lee et al., 2017) Lee, W., Song, K., & Moon, I. C. (2017, November). Augmented variational autoencoders for collaborative filtering with auxiliary information. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management (pp. 1139-1148).

• (Li et al., 2017) Li, D., Chen, C., Liu, W., Lu, T., Gu, N., & Chu, S. (2017). Mixture-rank matrix approximation for collaborative filtering. Advances in Neural Information Processing Systems, 30.

• (Saraswathi et a., 2017) Saraswathi, K., Saravanan, B., Suresh, Y., & Senthilkumar, J. (2017, November). Survey: a hybrid approach to solve cold-start problem in online recommendation system. In Proceedings of the International Conference on Intelligent Computing Systems (ICICS 2017–Dec 15th-16th 2017) organized by Sona College of Technology, Salem, Tamilnadu, India.

• (Volkovs et al., 2017) Volkovs, M., Yu, G., & Poutanen, T. (2017). Dropoutnet: Addressing cold start in recommender systems. Advances in neural information processing systems, 30.

• (Du et al., 2018) Du, C., Li, C., Zheng, Y., Zhu, J., & Zhang, B. (2018, April). Collaborative filtering with user-item co-autoregressive models. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 32, No. 1).

• (Lian et al., 2018) Lian, J., Zhou, X., Zhang, F., Chen, Z., Xie, X., & Sun, G. (2018, July). xdeepfm: Combining explicit and implicit feature interactions for recommender systems. In Proceedings of the 24th ACM SIGKDD international conference on knowledge discovery & data mining (pp. 1754-1763).

• (Liang et al., 2018) Liang, D., Krishnan, R. G., Hoffman, M. D., & Jebara, T. (2018, April). Variational autoencoders for collaborative filtering. In Proceedings of the 2018 world wide web conference (pp. 689-698).

• (Pimentel-Alarcón 2018) Pimentel-Alarcón, D. (2018). Mixture matrix completion. Advances in Neural Information Processing Systems, 31.

• (Prokhorenkova et al., 2018) Prokhorenkova, L., Gusev, G., Vorobev, A., Dorogush, A. V., & Gulin, A. (2018). CatBoost: unbiased boosting with categorical features. Advances in neural information processing systems, 31.

• (Ban et al., 2019) Ban, F., Woodruff, D., & Zhang, R. (2019). Regularized weighted low rank approximation. Advances in neural information processing systems, 32.

• (Chen et al., 2019) Chen, Y., Chen, B., He, X., Gao, C., Li, Y., Lou, J. G., & Wang, Y. (2019, July). λopt: Learn to regularize recommender models in finer levels. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (pp. 978-986).

• (Popov et al., 2019) Popov, S., Morozov, S., & Babenko, A. (2019). Neural oblivious decision ensembles for deep learning on tabular data. arXiv preprint arXiv:1909.06312.

• (Rama et al., 2019) Rama, K., Kumar, P., & Bhasker, B. (2019). Deep learning to address candidate generation and cold start challenges in recommender systems: A research survey. arXiv preprint arXiv:1907.08674.

• (Sachdeva et al., 2019) Sachdeva, N., Manco, G., Ritacco, E., & Pudi, V. (2019, January). Sequential variational autoencoders for collaborative filtering. In Proceedings of the twelfth ACM international conference on web search and data mining (pp. 600-608).

• (Song et al., 2019) Song, W., Shi, C., Xiao, Z., Duan, Z., Xu, Y., Zhang, M., & Tang, J. (2019, November). Autoint: Automatic feature interaction learning via self-attentive neural networks. In Proceedings of the 28th ACM international conference on information and knowledge management (pp. 1161-1170).

• (Huang et al., 2020) Huang, X., Khetan, A., Cvitkovic, M., & Karnin, Z. (2020). Tabtransformer: Tabular data modeling using contextual embeddings. arXiv preprint arXiv:2012.06678.

• (Rendle et al., 2020) Rendle, S., Krichene, W., Zhang, L., & Anderson, J. (2020, September). Neural collaborative filtering vs. matrix factorization revisited. In Proceedings of the 14th ACM Conference on Recommender Systems (pp. 240-248).

• (Schifferer et al., 2020) Schifferer, B., Titericz, G., Deotte, C., Henkel, C., Onodera, K., Liu, J., … & Erdem, A. (2020). GPU accelerated feature engineering and training for recommender systems. In Proceedings of the Recommender Systems Challenge 2020 (pp. 16-23).

• (Abdullah et al., 2021) Abdullah, N. A., Rasheed, R. A., Nasir, M. H. N. M., & Rahman, M. M. (2021). Eliciting auxiliary information for cold start user recommendation: A survey. Applied Sciences, 11(20), 9608.

• (Arik et al., 2021) Arik, S. Ö., & Pfister, T. (2021, May). Tabnet: Attentive interpretable tabular learning. In Proceedings of the AAAI conference on artificial intelligence (Vol. 35, No. 8, pp. 6679-6687).

• (Koren et al., 2021) Koren, Y., Rendle, S., & Bell, R. (2021). Advances in collaborative filtering. Recommender systems handbook, 91-142.

• (Sethi et al., 2021) Sethi, R., & Mehrotra, M. (2021). Cold start in recommender systems—A survey from domain perspective. In Intelligent Data Communication Technologies and Internet of Things: Proceedings of ICICI 2020 (pp. 223-232). Springer Singapore.

• (Yi et al., 2021) Yi, J., Kim, B., & Chang, B. (2021, December). Embedding Normalization: Significance Preserving Feature Normalization for Click-Through Rate Prediction. In 2021 International Conference on Data Mining Workshops (ICDMW) (pp. 75-84). IEEE.

• (Yi et al., 2021a) Yi, J., & Chang, B. (2021). Efficient Click-Through Rate Prediction for Developing Countries via Tabular Learning. arXiv preprint arXiv:2104.07553.

• (Borisov et al., 2022) Borisov, V., Leemann, T., Seßler, K., Haug, J., Pawelczyk, M., & Kasneci, G. (2022). Deep neural networks and tabular data: A survey. IEEE Transactions on Neural Networks and Learning Systems.

• (Panda et al., 2022) Panda, D. K., & Ray, S. (2022). Approaches and algorithms to mitigate cold start problems in recommender systems: a systematic literature review. Journal of Intelligent Information Systems, 59(2), 341-366.

• (Vančura et al., 2022) Vančura, V., Alves, R., Kasalický, P., & Kordík, P. (2022, September). Scalable linear shallow autoencoder for collaborative filtering. In Proceedings of the 16th ACM Conference on Recommender Systems (pp. 604-609).

• (Wang et al., 2022) Wang, Z., & Sun, J. (2022). Transtab: Learning transferable tabular transformers across tables. Advances in Neural Information Processing Systems, 35, 2902-2915.

• (Berisha et al., 2023) Berisha, F., & Bytyçi, E. (2023). Addressing cold start in recommender systems with neural networks: a literature survey. International Journal of Computers and Applications, 45(7-8), 485-496.

• (Liu et al., 2023) Liu, S., Liu, J., Gu, H., Li, D., Lu, T., Zhang, P., & Gu, N. (2023, October). Autoseqrec: Autoencoder for efficient sequential recommendation. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management (pp. 1493-1502).

• (Shin et al., 2023) Shin, K., Kwak, H., Kim, S. Y., Ramström, M. N., Jeong, J., Ha, J. W., & Kim, K. M. (2023, June). Scaling law for recommendation models: Towards general-purpose user representations. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 37, No. 4, pp. 4596-4604).

• (Spišák et al., 2023) Spišák, M., Bartyzal, R., Hoskovec, A., Peska, L., & Tůma, M. (2023, September). Scalable approximate nonsymmetric autoencoder for collaborative filtering. In Proceedings of the 17th ACM Conference on Recommender Systems (pp. 763-770).