Survival Analysis (3/3)

지난 포스트에서는 Survival Analysis를 활용해 서비스 이탈 현황을 분석하고 미래 이탈을 예측하는 방법을 살펴봤습니다. 이번 포스트에서는 지난 포스트에 등장한 여러 이론 중 빠진 내용을 보충 설명합니다.

기본 개념

Survival Function (생존함수)

생존함수는 관찰 대상이 특정 시간보다 더 오래 생존할 확률을 나타냅니다.

\[S(t)=\Pr(T>t)\]

\(\Pr\)은 확률이며, 시간 \(t\)는 함수에 전달하는 매개변수, 확률변수 \(T\)는 대상에 사건이 발생하는 시간입니다.

시작 시점(\(t = 0\))에는 모두 살아 있으니 생존함숫값은 1입니다. \((i.e. S(0) = 1)\) 시간이 흐르면서 대상 중 일부가 사망(즉, 이탈)할 것이고 다시 되살아나지 않을 겁니다. 즉, 생존함숫값은 시간이 갈수록 감소하기만 합니다. \((i.e. S(u) \leq S(t), \enspace \textrm{where} \enspace u \geq t)\) 마지막으로, 종료 시점을 두지 않고 시간을 무한대로 늘리면 결국 모두가 사망합니다. \((i.e. S(t) \rightarrow 0 \enspace \textrm{as} \enspace t \rightarrow \infty)\) 물론 데드풀이라면 끝까지 살아남겠지만 😏

Lifetime Distribution Function (생애분포함수)

생애분포함수는 생존함수의 정반대 개념입니다. 관찰 대상이 특정 시간 안에 생애를 마감할 확률입니다.

\[F(t)=Pr(T\leq t)=1-S(t)\]

이 함수를 미분하면 각 시간의 사건 발생율을 의미하는 Event density function(사건밀도함수)이 됩니다.

\[f(t)=F'(t)=\frac{d}{dt} F(t)\]

Survival Event Density Function (생존밀도함수)

생애분포함수와 사건밀도함수를 사용해 생존함수를 표현할 수 있습니다.

\[S(t)=\Pr(T>t)=\int_{t}^{\infty}{f(u)du}=1-F(t)\]

결국 생존함수(대상이 시간 \(t\)보다 더 오래 생존할 확률)는 시간 \(t\) 이후에 사건이 발생할 확률을 적분, 즉 모두 더한 것입니다. 생존함수를 미분하면 생존밀도함수를 구할 수 있으며, 사건밀도함수의 정반대 개념입니다.

\[s(t)=S'(t)=\frac{d}{dt}\int_{t}^{\infty}{f(u)du}=\frac{d}{dt}[1-F(t)]=-f(t)\]

Hazard Function (위험함수)

위험함수는 특정 시간 \(t\)에 사건(즉, 사망 또는 이탈)이 발생할 확률입니다. 다시 말해 대상이 시간 \(t\)까지 생존한 상태에서 정확히 \(t\) 시점에 사망할 확률이죠.

\[h(t)=\lim_{dt \rightarrow 0}{\frac{\Pr(t \leq T<t+dt)}{dt \cdot S(t)}}=\frac{f(t)}{S(t)}=-\frac{S'(t)}{S(t)}=-\frac{d}{dt}\log S(t)\]

위험함수는 시간 \(t\)에 사건이 발생할 확률을 시간 \(t\)보다 더 오래 생존한 확률로 나눈 결과로, 결국 생존함수에 로그를 적용하고 미분한 것과 같습니다. 따라서 위험함숫값은 항상 양수이며, 시간이 갈수록 늘어나거나 줄어들 수도 있고, 연속값이 아닐 수도 있습니다. 즉, 어떤 시간 구간에서는 전혀 사망(이탈)하지 않을 수도 있죠.

Cumulative Hazard Function (누적위험함수)

위험함수를 0부터 시간 \(t\)까지 적분하면 누적위험함수를 얻을 수 있습니다. 즉, 시간 \(t\)까지 사건이 발생할 확률을 모두 더한 것입니다.

\[H(t)=\int_{0}^{t}{h(u)du}=-\log S(t)\]

결국 생존함수, 생애분포함수, 누적위험함수는 다음 관계를 가집니다.

\[S(t)=\exp [-H(t)]=1-F(t), \quad t>0\]

Metrics

이제 이탈 예측의 정확도 지표를 알아봅시다. 지난 2편에서는 C-index를 사용했지만 다른 지표도 있습니다.

Concordance Index (C-index)

Survival Analysis에서 가장 많이 사용하는 정확도 지표입니다. 대상의 정확한 생존 시간을 평가하지 않고, 대신 여러 대상의 생존 시간(또는 위험)을 상대적으로 비교합니다. 즉, 사망 순서를 잘 예측하는지 판단합니다.

아래는 대상 한 쌍을 비교하는 Corcordance probability를 정의한 공식입니다. \(y_i\)는 사건이 발생한 실제 시각이며, \(\hat{y_i}\)는 모델이 예측한 시각입니다.

\[c=\Pr(\hat{y_1} > \hat{y_2} \mid y_1 \geq y_2)\]

이 정의를 바탕으로 C-index를 아래와 같이 계산할 수 있습니다.

\[\hat{c}=\frac{1}{P'}\sum_{i:\delta_i=1}\sum_{j:y_i<y_j}I[S(\hat{y_i} \mid X_i)<S(\hat{y_j} \mid X_j)]\]

\(P'\)는 평가 대상 쌍 개수이며, \(I\)는 주어진 조건이 참인 경우를 세는 indicator 함수입니다. 다시 말해 전체 평가 대상 쌍 중 대상 \(i\)보다 오래 생존한 대상 \(j\)의 생존함수를 더 크게 예측한 쌍의 비율을 계산하며, 0과 1 사이의 값을 가집니다. 집계 조건 중 \(\delta_i = 1\)은 대상 \(i\)에 반드시 사건(즉, 이탈)이 발생해야 한다는 의미입니다. 반대로 대상 \(i\)에 사건이 발생하기 전에 중도절단됐다면 대상 \(j\)가 대상 \(i\)보다 오래 생존했다고 확신할 수 없기 때문에 비교 대상에서 제외합니다. \(P'\)는 결국 전체 비교 가능 쌍 중 대상 \(i\)에 사건이 발생한 쌍의 개수입니다.

Mean Absolute Error

예측한 생존시간을 단순히 실제값과 비교하는 것도 물론 가능합니다. 다음과 같이 MAE를 계산할 수 있습니다.

\[\textrm{MAE}=\frac{1}{N}\sum_{i=1}^{N}{\delta_i|y_i-\hat{y_i}|}\]

마찬가지로 \(\delta_i\)가 1이면 사건(즉, 이탈)이 발생한 대상이며 0이면 중도절단된 대상입니다. 즉, 사건이 발생한 대상만 고려해 정확도를 계산합니다.

Survival Prediction Methods

Non-parametric Methods

Kaplan-Meier Estimation

지난 1편에서 소개한 Kaplan-Meier estimation은 데이터에서 생존함수를 추정하는 방법입니다. 멋진 이름에 비해 공식은 상당히 단순합니다.

\[\hat{S}(t)=\prod_{i:t_i \leq t}{\left(1-\frac{d_i}{n_i}\right)}\]

\(t_i\)는 주어진 시각 \(t\)보다 이전에 사건 발생한 시각입니다. \(n_i\)는 해당 시각 \(t_i\)까지 생존한 대상의 수이며 \(d_i\)는 이 시각에 사망한 수입니다. 결국 이 공식은 매시각 생존 비율을 계속 곱합니다.

Nelson-Aalen Estimation

Nelson-Aalen estimation은 반대로 누적위험함수를 추정합니다. 공식은 더 간단합니다. 매시각 남은 생존자 중 사망자의 비율을 계속 더합니다. 이런 간단한 공식으로 세상에 이름을 남길 수 있다니…일찍 태어날 걸 그랬습니다.

\[\hat{H}(t)=\sum_{t_i \leq t}{\frac{d_i}{n_i}}\]

Semi-parametric Methods

Cox Proportional Hazard (Cox PH) Model

지난 2편에서 소개했던 Cox PH 모델은 위험함수를 다음 공식으로 정의합니다.

\[h(t \mid X_i)=h_0(t) \exp(\beta_1x_{i1}+\cdots +\beta_px_{ip})=h_0(t)\exp (X_i \cdot \beta)\]

\(h_0\)는 시간에 따라 변화하는 baseline hazard function(기저위험함수)입니다. \(X_i\)는 대상 \(i\)의 변수(feature)이며, \(\beta\)는 모델이 학습해야 할 계수(coefficient)입니다.

공식을 보면 변수와 계수에 시간 \(t\)가 없다는 것을 알 수 있습니다. Cox PH 모델은 변수가 생존에 영향을 주지만 그 영향은 시간과 관계없다고 가정합니다. 예를 들어 흡연자는 비흡연자보다 사망 위험이 높지만 담배를 갓 피우기 시작한 대학생이나 30년 넘게 피운 중년이나 동일하게 위험하다고 가정합니다. (좋은 가정이 아닌 것 같죠?) 아래 공식을 보면 두 대상의 위험 비율이 시간, 그리고 시간에 따라 변화하는 기저위험함수와 독립적이라는 것을 알 수 있습니다.

\[\frac{h(t \mid X_1)}{h(t \mid X_2)}=\frac{h_0(t)\exp(X_1 \cdot \beta)}{h_0(t)\exp(X_2 \cdot \beta)}=\exp[(X_1-X_2) \cdot \beta]\]

따라서 Cox PH 모델은 기저위험함수를 무시하고, 다음과 같은 partial likelihood function을 사용해 계수 \(\beta\)를 학습합니다.

\[L(\beta)=\prod_{i:\delta_i=1}{\frac{h(y_i \mid X_i)}{\sum_{j:y_j \geq y_i}{h(y_i \mid X_j)}}}=\prod_{i:\delta_i=1}{\frac{\exp(X_i \cdot \beta)}{\sum_{j:y_j \geq y_i}{\exp(X_j \cdot \beta)}}}\]

직관적으로 \(\beta\)의 likelihood는 특정 시점에 대상 \(i\)가 사망했을때 그때까지 생존한 모든 다른 대상이 그 시점에 사망할 확률 중 대상 \(i\)가 사망할 확률입니다. 이 likelihood 함수를 아래와 같이 log likelihood function으로 바꿔 사용합니다.

\[\ell(\beta)=\sum_{i:\delta_i=1}{\left(X_i \cdot \beta - \log\left[\sum_{j:y_j \geq y_i}{\exp(X_j \cdot \beta)}\right]\right)}\]

Checking PH Assumption

앞서 언급했듯이 Cox PH 모델은 변수의 영향이 시간과 무관하다고 가정합니다. 따라서 Cox PH 모델로 생존을 예측하려면 예측에 사용할 변수가 정말 시간과 무관한지 검증하는 것이 좋습니다.

파이썬 lifelines 패키지는 PH 가정이 입력 데이터에 적합한지 자동으로 검사하는 기능을 제공합니다. 2편에서 생성한 샘플 데이터 data를 사용해 봅시다.

from lifelines import CoxPHFitter

cox = CoxPHFitter()
cox.fit(data, duration_col='time', event_col='event', show_progress=True)
cox.check_assumptions(data, p_value_threshold=0.05, show_plots=True)

함수가 출력한 결과와 차트를 보면 age와 num_calls 변수가 테스트를 통과하지 못했다고 나올겁니다. 두 변수는 시간 변수를 일부러 섞어 생성했습니다. CoxPHFitter.check_assumptions 함수는 아래 차트와 함께 이 변수들을 처리하는 방법도 제안합니다.

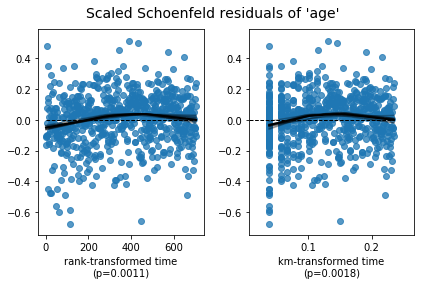
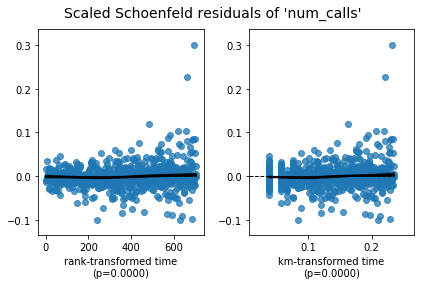
위 차트는 각 변수의 Schoenfeld residual을 그린 것입니다. Schoenfeld residual은 해당 시각에 이탈한 대상의 변숫값과 생존한 대상들로 계산한 기대값의 차이를 계산한 것입니다. 변숫값이 시간에 무관하고 모델이 \(\beta\)를 잘 추정했다면 Schoenfeld residual은 모든 시간에서 0에 되도록 가까워야 합니다. 하지만 위 차트의 일부 점들이 현저하게 벗어난 것을 볼 수 있습니다. 각 변수를 처리하는 방법은 lifelines 공식 문서를 참고하세요.

Parametric Methods

Parametric 예측 기법들은 생존시간이 특정 분포를 따른다고 가정하고 회귀 모델을 적용해 생존시간을 예측합니다. 주로 정규분포(normal), 지수분포(exponential), 베이불(Weibull) 분포, 로지스틱(logistic) 분포를 사용합니다. 다시 말해 다음과 같은 선형 모델을 가정하고, 시간 \(T\)와 오차항(noise term) \(\epsilon\)이 특정 분포를 따른다고 생각합니다.

\[T=X\cdot\beta+\epsilon\]

반면 생존시간에 로그를 적용한 값을 사용하기도 하며, Accelerated Failure Time (AFT) 모델이라고 부릅니다.

\[\ln(T)=X\cdot\beta+\epsilon\]

이렇게 로그를 적용하면 feature와 target, 즉 생존시간이 서로 multiplicative relationship을 가집니다. 예를 들어 선형 모델은 장기간 흡연 여부가 수명을 딱 10년 단축한다고 모델링한다면, AFT 모델은 10% 단축한다고 가정하는 것이죠. (10년과 10%는 아무 근거가 없는 숫자입니다. 오해 없길 바랍니다.)

이제 매개변수를 추정하는데 필요한 likelihood 함수를 알아봅시다. Likelihood 함수는 다음과 같이 사건밀도함수와 생존함수를 사용합니다.

\[L(\beta)=\prod_{\delta_i=1}{f(T_i, \beta)}\prod_{\delta_i=0}{S(T_i, \beta)}\]

공식에서 볼 수 있듯이, 학습 데이터셋은 사건이 발생한 대상들(\(\delta=1\))과 중도절단된 대상들(\(\delta=0\))로 나눌 수 있습니다. 사건이 발생한 대상은 관측된 사건 발생 시각(\(T_i\))에 사망했기 때문에 사건밀도함수가 1에 가까울 겁니다. 중도절단된 대상들은 언제 사망했는지 알 수 없지만, 최소한 기록된 시각(\(T_i\))까지는 생존했으므로 생존함수가 1에 가까울 겁니다. 따라서 모든 대상의 사건밀도함수 또는 생존함수 결과를 곱한 값을 가장 크게 만드는 \(\beta\) 값이 가장 좋은 매개변숫값이라고 생각할 수 있습니다.

사건밀도함수와 생존함수는 모델이 가정하는 분포에 따라 다릅니다. 예를 들어 exponential 분포를 가정한 AFT 모델은 위험함수를 단일 매개변수 \(\lambda\)로 설정합니다.

\[h(t)=\lambda=\exp(X \cdot \beta)\] \[f(t)=h(t)S(t)=\lambda\exp(-H(t))=\lambda\exp(-\lambda t)\] \[L=\prod_{\delta_i=1}{f(T_i)}\prod_{\delta_i=0}{S(T_i)}=\prod_{\delta_i=1}{[\lambda\exp(-\lambda t)]}\prod_{\delta_i=0}{[\exp(-\lambda t)]}\]

마무리

지금까지 생존분석 및 예측의 이론적인 내용을 살펴봤습니다. 하지만 모든 알고리즘을 다 소개한 것은 아닙니다. 관심이 있다면 관련 논문을 더 찾아보기 바랍니다.

그러나 알고리즘 이론보다 더 중요한 것은 알고리즘을 실제로 적용하고 의미있는 성과를 내는 것이라 봅니다. 다음에는 하이퍼커넥트의 성과를 소개할 수 있기를 바라며 이번 포스트를 마칩니다.