A/B 테스트 자동 분석툴 개발하기

안녕하세요, 하이퍼커넥트에서 data scientist로 근무하는 성혁화입니다.

Data-Driven 회사에서는 수많은 의사결정이 사람의 직관이 아닌 A/B 테스트를 통해 이루어집니다. 이때 A/B 테스트의 두 집단의 지표를 정확하게 비교(어느 집단이 유의하게 좋은지)하는 일은 의사결정에 있어 매우 중요합니다. 또한, A/B 테스트의 지표 분석 및 유의성 검증은 반복되는 작업으로 분석가의 시간이 요구됩니다. 따라서 정확하면서도 자동화된 A/B Test 분석 툴이 있다면 유용할 것입니다.

이 글에서는 자동 분석 툴을 만들기 위해선 무엇이 중요한지, 어떻게 정확도를 올리고 자동화를 시켰는지에 대해 소개합니다.
*Bayesian Inference, Markov chain Monte Carlo(MCMC)에 대한 기본적인 지식이 있다고 가정합니다.

관측 데이터의 분포에 대한 가정이 중요하다

정확하면서도 자동화된 분석 툴을 만들기 위해서는 무엇보다도 관측 데이터의 분포에 대해 고민하는 게 가장 중요합니다. 프로모션에 두 가지 옵션이 있어 어떤 옵션이 더 좋은지 A/B 테스트를 통해서 검정해보는 경우를 생각해 봅시다. A/B 테스트에서는 다음과 같은 결과를 얻었습니다.

	유저수	관측 데이터(결제액)	평균
A	1000	100000원 10명, 0원 990명	1000원
B	1000	9000원 100명, 0원 900명	900원

그룹 A의 인당 평균 결제액은 1000원이며 그룹 B는 900원임을 알 수 있습니다. 각 그룹 간의 평균 결제액을 확인해 보았더니 그룹 A가 그룹 B보다 100원 높게 나왔네요. 결과를 보고 다음과 같은 질문을 할 수 있습니다.

그룹 A의 옵션이 그룹 B의 옵션보다 좋을까?
그룹 A가 그룹 B보다 유의하게 좋을까?
평균과는 반대로 그룹 B가 그룹 A보다 유의하게 좋을 수 있을까?

마지막 질문에 대해 의구심이 들 수도 있습니다.

‘A가 B보다 유의하게 좋지 않을 순 있어도 B가 A보다 유의하게 좋은 상황은 불가능하지 않을까?’

하지만 충분히 가능한 일입니다. 실제로 인당 결제액의 분포가 pareto 분포를 따른다고 가정하면 그룹 B가 그룹 A보다 유의하게 좋습니다. 반면 결제액의 분포를 normal 분포로 가정한다면 산술평균의 순서와 반대로 역전되는 결론은 나지 않습니다. 즉, 통계적 추론의 결론은 가정을 어떻게 하느냐에 따라 달라집니다.

이처럼 가정에 따라 통계적 추론의 결론이 다르기 때문에 올바른 결론을 내기 위해서는 ‘좋은’ 가정을 하는 것이 중요합니다. 어떤 가정이 좋은 것일까요? ‘좋다’의 정량적인 평가가 가능할까요?

이 글에서는

좋은 가정을 찾는 방법
분석 툴 사용자가 1번에 대한 고민 전혀 없이 분석 결과를 얻을 수 있는 자동화 방법

에 대해 순서대로 다룰 것입니다.

관측 데이터에 대한 가정이 중요하다 2

‘매출 데이터는 normal 분포라고 가정하면 안 좋다는 건 알겠는데, 그럼 pareto 분포로 가정하는 정도로 충분하지 않을까?’ 라고 생각할 수 있습니다. 하지만 그렇지 않다는 것은 간단한 실험을 통해서 알 수 있습니다.

1000만 명의 매출 데이터를 모집단으로 준비합니다. 여기서 복원추출로 한 그룹당 10만 명씩 랜덤하게 뽑는 행위를 반복해 10개의 그룹을 만들어 봅시다. 그 후 각 그룹의 mean의 분포 구해봅시다.

mean의 분포는 당연히 데이터의 분포를 어떻게 가정하냐에 따라 달라지는데, pareto 분포를 가정하면 다음과 같이 됩니다.

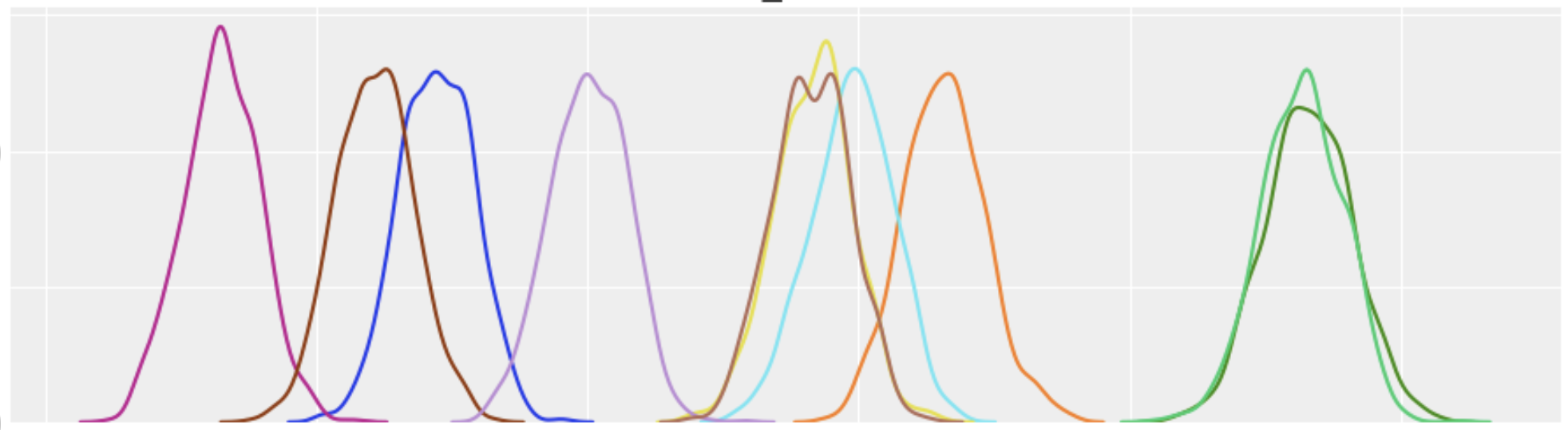
같은 모집단에서 샘플링한 그룹들이었음에도 불구하고 mean이 유의미하게 다른 것처럼 나오게 됩니다. 분포에 대한 잘못된 가정으로 인해 잘못된 결과가 도출된 것입니다. 실험이 아니라 실제 상황에서 매출 데이터를 pareto 분포로 해석했다면 A가 B보다 유의하게 좋지 않음에도 불구하고 좋다고 해석하거나 반대의 경우도 가능하겠죠.

제가 매출 데이터의 분포로 가장 많이 사용하는 어떤 Mixture 분포는(0-constant 분포와 Weibull 분포로 이루어진 Mixture) 매출 데이터 분포에 대한 가정이 pareto보다 더 정확하기 때문에 위와 같은 상황이 거의 없습니다.

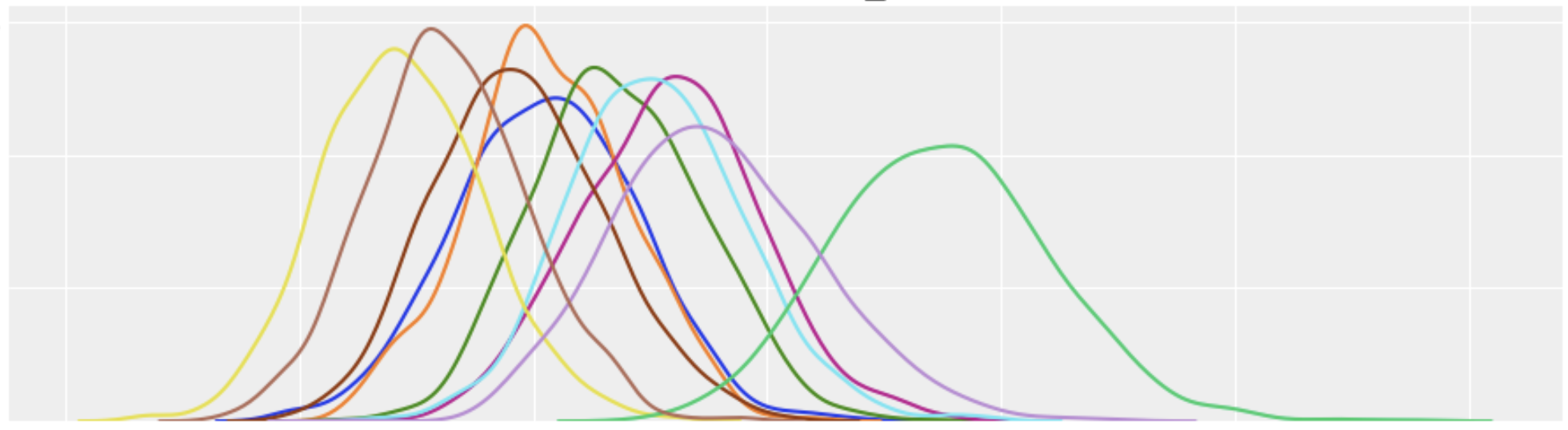
10개의 그룹 모두 서로 유의하게 좋거나 나쁜 관계는 없다고 나오네요. 이처럼 좋은 가정을 찾는 것은 A/B 테스트 후 의사결정에 있어 매우 중요하다고 할 수 있습니다.

Bayesian model 학습 예제

일단, 베이지안 추론은 어떻게 할 수 있는지 예제를 통해 간단하게 알아보겠습니다. Bayesian model을 학습시켜주는 python 라이브러리인 pymc3을 사용하였습니다. 예제 데이터는 평균이 10, 분산이 3인 normal 분포에서 10000개를 샘플링해서 만들어 보겠습니다.

from scipy.stats import norm

data = norm.rvs(loc=10, scale=3, size=10000)

관측 데이터를 normal 분포라고 가정했을 때의 Bayesian model을 pymc3로 설계하면 다음과 같습니다.

import pymc3 as pm
with pm.Model() as model:
    mu = pm.Normal("mu", 0, sigma=100)
    simga = pm.Exponential('sigma', lam = 2.0)
    
    obs = pm.Normal("obs", mu=mu, sigma=simga, observed=data)

위의 코드를 해석하면 다음과 같습니다.

- 관측한 data는 normal 분포를 따른다.
- 해당 normal 분포의 mu와 sigma는 고정되어 있지 않고 확률변수이다.
- 확률변수 mu의 prior 분포는 평균이 0, 표준편차가 100인 normal 분포를 따른다고 가정하였다.
- 확률변수 sigma의 prior 분포는 lambda가 2인 exponential 분포를 따른다고 가정하였다.

model을 만들었으면 학습을 위해 아래와 같이 Markov chain Monte Carlo(MCMC)를 수행해 주면 됩니다.

with model:
    trace = pm.sample(1000)

trace에는 mu, sigma의 샘플이 각각 1000개씩 들어가게 되고 그 샘플은 mu, sigma의 posterior 분포를 따르게 되죠.

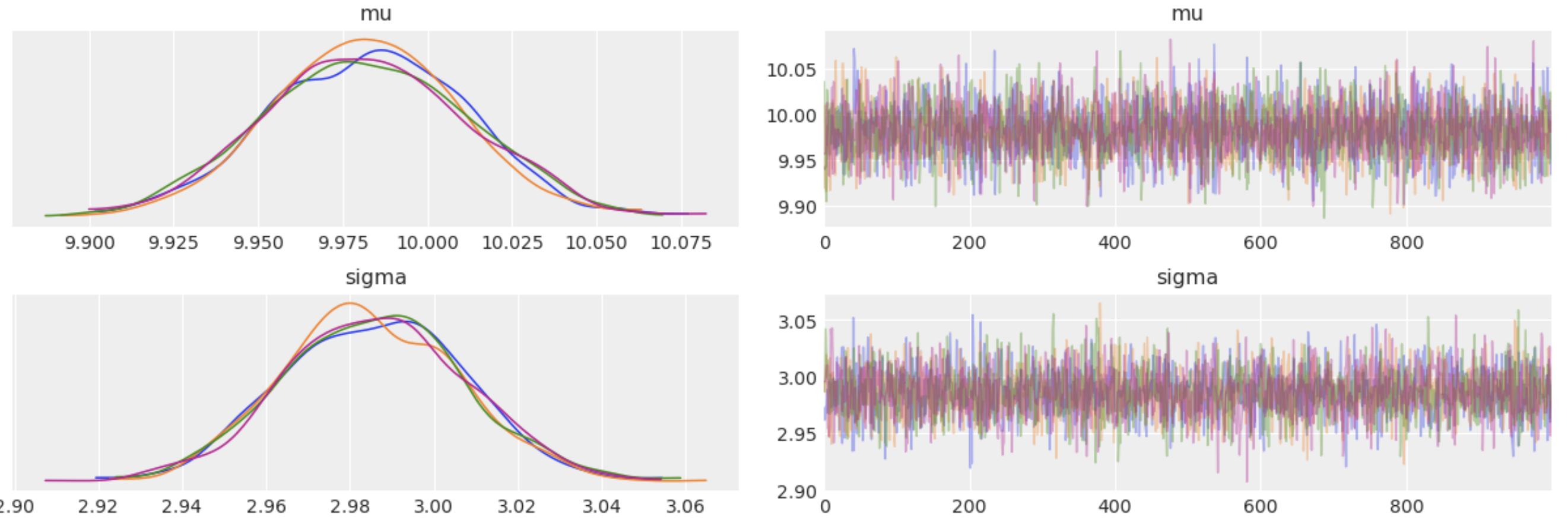
parameter의 posterior 분포가 있으면 mean의 분포를 직접 계산해서 구할 수 있습니다. normal의 경우 mu의 분포가 바로 mean의 분포가 되겠네요.

좋은 가정(모델)을 찾는 방법

분포에 대한 가정을 했을 때 Bayesian model을 어떻게 만들고 학습시키는지 간단히 알아보았습니다. 가정에 따라 Bayesian model이 달라질 텐데 관측 데이터에 적합한 ‘좋은’ Bayesian model은 어떻게 찾을까요?

일반적으로 machine learning에서 model 간의 비교를 위해서는 cross-validation을 사용합니다. 특히 k-fold cross validation을 많이 사용하죠. LOO(Leave-one-out) cross validation도 있지만 re-fitting 횟수가 전자는 k 번, 후자는 데이터의 개수만큼(!!) 필요하기 때문에 전자를 주로 사용합니다. 하지만 MCMC Sample들로 re-fitting을 하지 않고도 효율적으로 LOO CV를 하는 방법이 제안되어 있고 arviz 라이브러리에 구현되어 있어 편리하게 사용할 수 있습니다.

이제 어떤 모델이 매출 데이터에 적합한지 정량적으로 확인해 보겠습니다. Bayesian model의 후보로 아래의 5개를 골랐습니다.

Normal, Pareto, Weibull : 각각 Normal, Pareto, Weibull 분포
Mixture - Pareto : 0-constant 분포와 pareto 분포의 mixture
Mixture - Weibull : 0-constant 분포와 weibull 분포의 mixture

arviz 라이브러리의 compare 함수를 사용하여 각 Bayesian model의 LOO CV 값을 구할 수 있는데, 입력으로 각 모델의 MCMC Sample이 필요합니다.

import arviz as az
df_comp_loo = az.compare({
    'Normal': trace_normal,
    'Pareto': trace_pareto,
    'Weibull': trace_weibull,
    'Mixture - Pareto': trace_mix_pareto,
    'Mixture - Weibull': trace_mix_weibull
})
df_comp_loo

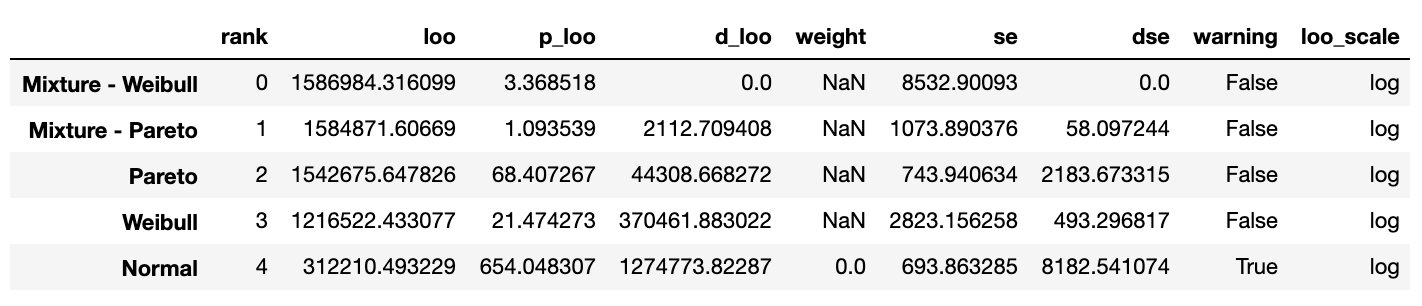
rank는 각 모델들의 CV 결과에 따른 랭킹을 나타냅니다. LOO는 LOO CV 값을 나타냅니다.

위의 결과를 plot으로도 확인할 수 있습니다.

az.plot_compare(df_comp_loo, insample_dev=False);

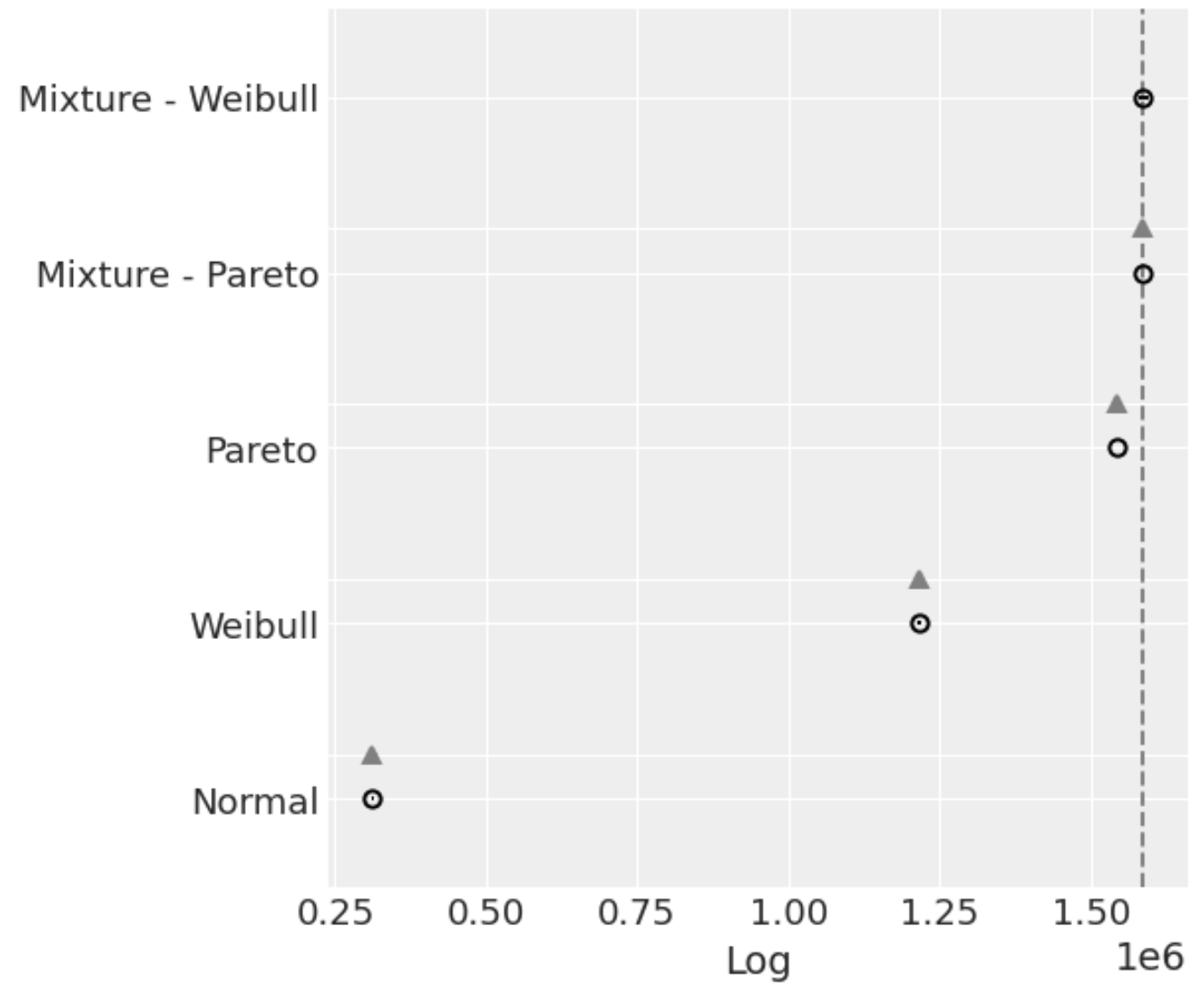
동그라미는 각 모델들의 LOO CV 값을 나타냅니다. 원래 동그라미 좌우로 standard error가 표시되는데 이번엔 오차가 너무 작아서 보이지 않네요. 위의 테이블과 plot을 토대로 해당 Mixture - Weibull 모델이 매출 데이터를 제일 잘 설명함을 확인할 수 있었습니다.

자동으로 모델 정하기

데이터가 주어졌을 때 LOO CV를 이용하여 최적의 Bayesian model을 찾는 방법을 알아보았습니다. 그렇다면 다른 모양의 분포를 가지는 데이터가 들어오면 어떻게 될까요. 매출 데이터의 분포와 유사한 모양이 아닌, Normal 분포나 Pareto 분포가 들어올 수도 있을 것입니다. 당연히 normal 분포 모양의 데이터는 normal 분포로, pareto 분포 양의 데이터는 pareto로 가정하고 추론하는 게 가장 좋겠죠. 앞에서 나온 model 비교 방법을 응용하면 이 문제 또한 쉽게 해결할 수 있습니다.

아이디어는 이렇습니다.

“입력으로 들어올 수 있는 다양한 분포에 대해 각각 Bayesian model을 만들어 놓고 입력이 들어왔을 때 가능성이 가장 높은(LOO CV 값이 가장 큰) model을 사용한다”

매출 데이터는 Mixture - Weibull 분포가 LOO CV 값이 가장 좋게 나올 테니 Mixture - Weibull로 추론하고 Normal 분포 모양의 데이터는 Normal 분포가 LOO CV 값이 가장 좋게 나올 테니 Normal로 추론하게 되는 것입니다. 여러 분포 중에서 관측 데이터에 가장 알맞는 분포를 자동으로 정해주게 되는 셈이죠.

마치며

지금까지의 내용을 토대로 A/B test 자동 분석 툴을 만들 수 있습니다. 데이터의 분포를 자동으로 정하고 어떤 그룹이 더 좋을지 추론까지 전부 해주기 때문에 분석 툴 사용자 입장에서는 편리하고 정확한 블랙박스가 됩니다.

포스트는 여기까지입니다. 감사합니다.